Heat Transfer Miscellaneous
- The average heat transfer coefficient on a thin hot vertical -plate suspended in still air can be determined from observations of the change in plate temperature with time as it cools. Assume the plate temperature to be uniform at any instant of time and radiation heat exchange with the surroundings negligible. The ambient temperature is 25°C, the plate has a total surface area of 0.1 m2 and a mass of 4 kg. The specific heat of the plate material is 2.5 kJ/kgK. The convective heat transfer coefficient in W/m2K, at the instant when the plate temperature is 225°C and the change in plate temperature with time dT/dt = – 0.02 K/s, is
-
View Hint View Answer Discuss in Forum
From heat balance equation,
-hA(T - T0) = mc dT dt
where, T0 = Ambient temperature∴ h = 4 × 2.5 × 103 × 0.2 = 10 W /m2 K 0.1 × 200 Correct Option: A
From heat balance equation,
-hA(T - T0) = mc dT dt
where, T0 = Ambient temperature∴ h = 4 × 2.5 × 103 × 0.2 = 10 W /m2 K 0.1 × 200
- A steel ball of 10 mm diameter at 1000 K is required to be cooled to 350 K by immersing it in a water environment at 300 K. The convective heat transfer coefficient is 1000 W/m2K. Thermal conductivity of steel is 40 W/m K. The time constant for the cooling process is 16 s. The time required (in s) to reach the final temperature is
-
View Hint View Answer Discuss in Forum
Biot Number = hLc = 0.458 K For sphere Lc = Volume = d surface area 6 ∴ Bi = hd = 1000 × 0.01 6K 6 × 40
= 0.0416 < 0.1
Hence lumped heat analysis is used
T - T∞ = exp 
-hAst 
= e -t Ti - T∞ ρ V Cp ṫ
Thermal time constant,t* = ρ V Cp = 16 sec hAs ∴ 350 - 300 = e -t 1000 - 300 16
⇒ t = 42.2249 secCorrect Option: A
Biot Number = hLc = 0.458 K For sphere Lc = Volume = d surface area 6 ∴ Bi = hd = 1000 × 0.01 6K 6 × 40
= 0.0416 < 0.1
Hence lumped heat analysis is used
T - T∞ = exp 
-hAst 
= e -t Ti - T∞ ρ V Cp ṫ
Thermal time constant,t* = ρ V Cp = 16 sec hAs ∴ 350 - 300 = e -t 1000 - 300 16
⇒ t = 42.2249 sec
- Consider the radiation heat exchange inside an annulus between two very long concentric cylinders. The radius of the outer cylinder is R0 and that of the inner cylinder is Ri. The radiation view factor of the outer cylinder onto itself is
-
View Hint View Answer Discuss in Forum
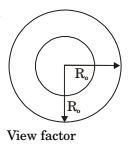
F1– 1 = 0
F1– 2 = 1
Reciprocacy theorem
A2 F2– 1 = A1 F1– 2⇒ F2– 1 = A1 F1– 2 A2 = 2πRiL = Ri 2πRoL Ro
F2– 1 + F2– 2 = 1∴ F2– 2 = 1 - F2– 1 = 1 - Ri Ro
Correct Option: D

F1– 1 = 0
F1– 2 = 1
Reciprocacy theorem
A2 F2– 1 = A1 F1– 2⇒ F2– 1 = A1 F1– 2 A2 = 2πRiL = Ri 2πRoL Ro
F2– 1 + F2– 2 = 1∴ F2– 2 = 1 - F2– 1 = 1 - Ri Ro
- Sphere 1 with a diameter of 0.1 m is completely enclosed by another sphere 2 of diameter 0.4 m. The view factor F12 is
-
View Hint View Answer Discuss in Forum
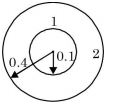
F11 = 0
F12 = 1Correct Option: D

F11 = 0
F12 = 1
- Three sets of parallel plates LM, NR and PQ are given in Figures 1, 2 and 3. The view factor Fij is defined as the fraction of radiation leaving plate I that is intercepted by plate J. Assume that the val ues of FL M and FN R ar e 0.8 and 0.4, respectively. The value of FPQ (round off to one decimal place) is _____.

-
View Hint View Answer Discuss in Forum

FLM = F(I) + F(II) + F(III)
Where F is shape factor of surface area I, II and III of M with surface area of ‘L’
0.8 = F(I) + F(II) + F(III)
∵ (I) and (III) are symmetrical in shape so, shape factor of these surface will be same i.e. F(I) = F(III)
So, 0.8 = 2F(I) + F(II)... (1)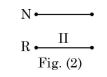
In this area (II) is same as fig. (I) area II.
i.e. FNR = F(II) = 0.4... (2)
From equation (1),F(III) = 0.8 - 0.4 = 0.2 2 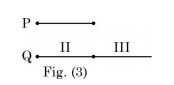
Here, FPQ = F(II) + F(III)
= 0.4 + 0.2 = 0.6
Correct Option: B

FLM = F(I) + F(II) + F(III)
Where F is shape factor of surface area I, II and III of M with surface area of ‘L’
0.8 = F(I) + F(II) + F(III)
∵ (I) and (III) are symmetrical in shape so, shape factor of these surface will be same i.e. F(I) = F(III)
So, 0.8 = 2F(I) + F(II)... (1)
In this area (II) is same as fig. (I) area II.
i.e. FNR = F(II) = 0.4... (2)
From equation (1),F(III) = 0.8 - 0.4 = 0.2 2 
Here, FPQ = F(II) + F(III)
= 0.4 + 0.2 = 0.6

