Heat Transfer Miscellaneous
- A slender rod of length L, diameter d (L >> d) and thermal conductivity k1 i s joined with another rod of identical dimensions, but of thermal conductivity k 2, to form a composite cylindrical rod of length 2L. The heat transfer in radial direction and contact resistance are negligible. The effective thermal conductivity of the composite rod is
-
View Hint View Answer Discuss in Forum
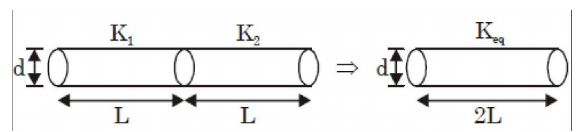
As per question, heat transfer in radial direction and contact resistance are negligible. In series connection,
(Rth) eq = R1 + R22L = L + L Akeq AK1 AK2 2 = 1 + 1 Keq K1 K2 ⇒ Req = 2K1K2 K1 + K2 Correct Option: A

As per question, heat transfer in radial direction and contact resistance are negligible. In series connection,
(Rth) eq = R1 + R22L = L + L Akeq AK1 AK2 2 = 1 + 1 Keq K1 K2 ⇒ Req = 2K1K2 K1 + K2
- The peak wavelength of radiation emitted by a black body at a temperature of 2000 K is 1.45 μm. If the peak wavelength of emitted radiation changes to 2.90 μm, then the temperature (in K) of the black body is
-
View Hint View Answer Discuss in Forum
From wein’s displacement law λmax T = constant
(λmax)1 T1 = (λmax)2 T2
1.45 × 2000 = 2.90 × T2T2 = 
1.45 × 2000 
2.90
T2 = 1000 KCorrect Option: B
From wein’s displacement law λmax T = constant
(λmax)1 T1 = (λmax)2 T2
1.45 × 2000 = 2.90 × T2T2 = 
1.45 × 2000 
2.90
T2 = 1000 K
- A balanced counter flow heat exchanger has a surface area of 20 m2 and overall heat transfer coefficient of 20 W/m2K. Air (cp = 1000 J/kgK) entering at 0.4 kg/s and 280 K is to be preheated by the air leaving the system at 0.4 kg/s and 300 K. The temperature (in K) of the preheated air is
-
View Hint View Answer Discuss in Forum
Counter flow heat exchanged
Surface Area A = 20 m2, mass flow rate = 0.4 kg/su = 20W ; m2
Temperature Tci = 280KCp of air = 1000 1 kg K 
Since m is same for both flow = 0.4 kg/s
Assume Cp is same = 100 J/kg.K
Hence ∆T1 = Tci – Tco = ∆T2 = Th0 – Tci
∆T1 = 300 – Tco = Th0 – 280
∆Tm = ∆T1 = ∆T2
uA∆Tm = mCp (Tco – Tci)
20 × 20 × (300 – Tco) = 0.4 × 1000(Tco – 280)
2Tco = 300 + 280Tco = 580 = 290 K 2 Correct Option: A
Counter flow heat exchanged
Surface Area A = 20 m2, mass flow rate = 0.4 kg/su = 20W ; m2
Temperature Tci = 280KCp of air = 1000 1 kg K 
Since m is same for both flow = 0.4 kg/s
Assume Cp is same = 100 J/kg.K
Hence ∆T1 = Tci – Tco = ∆T2 = Th0 – Tci
∆T1 = 300 – Tco = Th0 – 280
∆Tm = ∆T1 = ∆T2
uA∆Tm = mCp (Tco – Tci)
20 × 20 × (300 – Tco) = 0.4 × 1000(Tco – 280)
2Tco = 300 + 280Tco = 580 = 290 K 2
- Consider a parallel-flow heat exchanger with area Ap and a counter-flow heat exchanger with area Ac. In both the heat exchangers, the hot stream flowing at 1 kg/s cools from 80°C to 50°C. For the cold stream in both the heat exchangers, the flow rate and the inlet temperature are 2 kg/s and 10°C, respectively. The hot and cold streams in both the heat exchangers are of the same fluid. Also, both the heat exchangers have the same overall heat transfer coefficient. The ratio Ac /Ap is _____.
-
View Hint View Answer Discuss in Forum

Correct Option: A

- In a counter-flow heat exchanger, water is heated at the rate of 1.5 kg/s from 40°C to 80°C by an oil entering at 120°C and leaving at 60°C. The specific heats of water and oil are 4.2 kJ/ kgK and 2 kJ/kgK, respectively. The overall heat transfer coefficient is 400 W/m2K. The required heat transfer surface area (in m2) is
-
View Hint View Answer Discuss in Forum
Heat exchanger is a counterflow type.
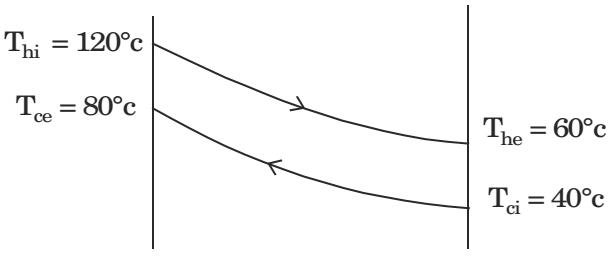
∆Ti = 120 – 80 = 40°C (θ1)
∆Te = 60 – 40 = 20°C (θ2)LMTD = θ1 - θ2 In 
θ1 
θ2 = 40 - 20 = 28.86°C In 
40 
20
Q = mc Cpc(Tce - Tci)
= 1.5 × 4.2 × 103 (80 – 40) watt
Q = 252000 W
Q = UA∆Tm .A = Q = 1.5 × 4.2 × 103 × 40 U∆Tm 400 × 28.86
= 21.83 m2.Correct Option: D
Heat exchanger is a counterflow type.

∆Ti = 120 – 80 = 40°C (θ1)
∆Te = 60 – 40 = 20°C (θ2)LMTD = θ1 - θ2 In 
θ1 
θ2 = 40 - 20 = 28.86°C In 
40 
20
Q = mc Cpc(Tce - Tci)
= 1.5 × 4.2 × 103 (80 – 40) watt
Q = 252000 W
Q = UA∆Tm .A = Q = 1.5 × 4.2 × 103 × 40 U∆Tm 400 × 28.86
= 21.83 m2.

