Heat Transfer Miscellaneous
- Lumped heat transfer analysis of a solid object suddenly exposed to a fluid medium at a different temp is valid when
-
View Hint View Answer Discuss in Forum
For lumed system analysis, Bi < 0.1
Correct Option: A
For lumed system analysis, Bi < 0.1
- For a hydrodynamically and ther mally fully developed laminar flow through a circular pipe of constant cross-section. The Nusselt number at constant wall heat flux (Nuq) and that at constant wall temperature (NuT) are related as
-
View Hint View Answer Discuss in Forum
(Nu)q for constant wall heat flux and (Nu)T at constant wall temperature for a hydrodynamically and t hermally fully developed laminar flow through a circular pipe of constant cross-section is 4.36 and 3.66 respectively. Hence, (Nu)q > (Nu)T
Correct Option: D
(Nu)q for constant wall heat flux and (Nu)T at constant wall temperature for a hydrodynamically and t hermally fully developed laminar flow through a circular pipe of constant cross-section is 4.36 and 3.66 respectively. Hence, (Nu)q > (Nu)T
- The wall of a constant diameter pipe of length 1 m is heated uniformly with flux q” by wrapping a heater coil around it. The flow at the inlet to the pipe is hydrodynamically fully developed. The fluid is incompressible and the flow is assumed to be laminar and steady all through the pipe. The bulk temperature of the fluid is equal to 0°C at the i nlet and 50°C at the exi t. The wall temperatures are measured at three locations, P, Q and R as shown in the figure. The flow thermally develops after some distance from the inlet. The following measurements are made:
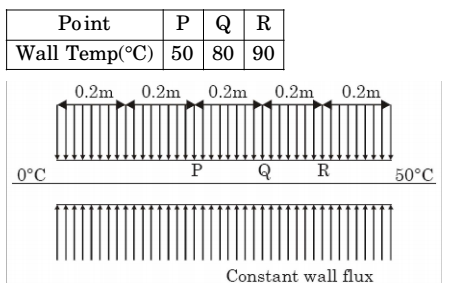
Among the locations P, Q and R, the flow is thermally at:
-
View Hint View Answer Discuss in Forum
I n case of uni for m heat flux, bulk mean t emperat ur e var ies linearly.
The difference bet ween bulk mean temperature and wall temperature is constant in thermally developed region so bulk tempeature,
T(x) = A + Bx
At x = 0, T = 0°C
⇒ A = 0°C
At x = 1, T = 50°C
⇒ B = 50°C
∴ T(x) = 50x
Here,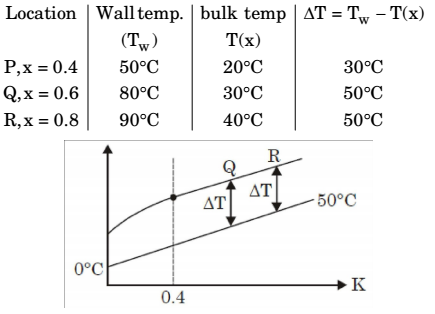
So, Q and R in thermally developed region.Correct Option: D
I n case of uni for m heat flux, bulk mean t emperat ur e var ies linearly.
The difference bet ween bulk mean temperature and wall temperature is constant in thermally developed region so bulk tempeature,
T(x) = A + Bx
At x = 0, T = 0°C
⇒ A = 0°C
At x = 1, T = 50°C
⇒ B = 50°C
∴ T(x) = 50x
Here,
So, Q and R in thermally developed region.
- Water flows through a tube of diameter 25 mm at an average velocity of 1.0 m/s. The properties of water are ρ = 1000 kg/m3, μ= 7.25 × 104 Ns/m², k = 0.625 W/mK, Pr = 4.85. Using Nu = 0.023 Re0.8 Pr0.4, the convective heat transfer coefficient (inW/m²K) is _______
-
View Hint View Answer Discuss in Forum
Re = ρvd μ = 1000 × 1 × 25 × 103 7.25 × 10-4
= 34482.75
Pr = 4.85
Nu = 0.023 Re0.8 Pr0.4.
Nu = .0.23 × (34482.758)0.8 (4.85)0.4.
= 184.546&Nu = hd k h = Nu.k d = 184.546 × 0.625 25 × 10-3 = 4613.66 W m²K
Correct Option: A
Re = ρvd μ = 1000 × 1 × 25 × 103 7.25 × 10-4
= 34482.75
Pr = 4.85
Nu = 0.023 Re0.8 Pr0.4.
Nu = .0.23 × (34482.758)0.8 (4.85)0.4.
= 184.546&Nu = hd k h = Nu.k d = 184.546 × 0.625 25 × 10-3 = 4613.66 W m²K
- In a condenser, water enters at 30°C and flows at the rate 1500 kg/hr. The condensing steam is at a temperature of 120°C and cooling water leaves the condenser at 80°C. Specific heat of water is 4.187 kJ/kgK. If the overall heat transfer coefficient is 2000 W/m2 K, the heat transfer area is
-
View Hint View Answer Discuss in Forum
Here, θ1 = 120 – 30 = 90ºC
θ2 = 120 – 80 = 40ºC
Log mean temperature difference,
Q = mcpw ∆T1500 × 1 × 4.187 × (50) × 103 3600
= 87.22 × 103 Joule/s
Again
Q = UAθm
or 87.22 × 103 = 2000 × A × 61.65
∴ A = 0.707 m2Correct Option: A
Here, θ1 = 120 – 30 = 90ºC
θ2 = 120 – 80 = 40ºC
Log mean temperature difference,
Q = mcpw ∆T1500 × 1 × 4.187 × (50) × 103 3600
= 87.22 × 103 Joule/s
Again
Q = UAθm
or 87.22 × 103 = 2000 × A × 61.65
∴ A = 0.707 m2

