76. A long glass cylinder of inner diameter = 0.03 m and outer diameter = 0.05 m carries hot fluid inside. If the thermal conductivity of glass = 1.05 W/mK, the thermal resistance (K/W) per unit length of the cylinder is

1. 1. 0.031

   
   
   

   2. 0.077

   
   
   

   3. 0.17

   
   
   

   4. 0.34

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Given data:
   d₁ = 0.03 m
   

   ∴ r1	d1	=	0.3	= 0.015 m
   	2		2

   
   d₂ = .05 m
   ∴ r₂ = .025 m
   

   K = 1.05	W
   	mK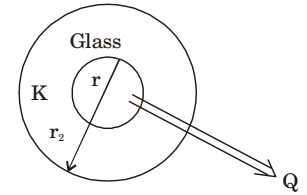

   
   
   Thermal resistance
   

   Rt =	1	loge		r2
   	2πKL			r1

   
   

   =	1	loge		.025
   	2 × 3.14 × 1.05 × 1			.015

   
   = 0.077 W/m

   Correct Option: B

   Given data:
   d₁ = 0.03 m
   

   ∴ r1	d1	=	0.3	= 0.015 m
   	2		2

   
   d₂ = .05 m
   ∴ r₂ = .025 m
   

   K = 1.05	W
   	mK

   
   
   Thermal resistance
   

   Rt =	1	loge		r2
   	2πKL			r1

   
   

   =	1	loge		.025
   	2 × 3.14 × 1.05 × 1			.015

   
   = 0.077 W/m

---

77. Consider a long cylindrical tube of inner and outer radii, r_i and r₀, respectively, length L and thermal conductivity, k. Its inner and outer surfaces are maintained at T_i, and T₀, respectively (T_i > T₀). Assuming one dimensional steady state heat conduction in the radial direction, the thermal resistance in the wall of the tube is

1. 1. 	1	In		ri
      	2πkL			r0

   
   
   

   2. L

      2πrik

   
   
   

   3. 	1	In		r0
      	2πkL			ri

   
   
   

   4. 	1	In		r0
      	4πkL			ri

   
   
   

---

1. View Hint View Answer Discuss in Forum

   A_r = 2πrL
   From Fourier ’s Law
   

   qr = kAr	dT
   	dr

   
   

   qr = 2π krL	dT
   	dr

   
   Boundary conditions:
   T = T_i at r = r_i
   T = T₀ at r = r₀
   

   q =	2πkL(Ti - T0)
   	In(r0/ri)

   
   
   

   Rth =	In(r0/ri)
   	2πkL

   Correct Option: C

   A_r = 2πrL
   From Fourier ’s Law
   

   qr = kAr	dT
   	dr

   
   

   qr = 2π krL	dT
   	dr

   
   Boundary conditions:
   T = T_i at r = r_i
   T = T₀ at r = r₀
   

   q =	2πkL(Ti - T0)
   	In(r0/ri)

   
   
   

   Rth =	In(r0/ri)
   	2πkL

---

---

78. A hollow cylinder has length L, inner radius r₁ outer radius r₂, and thermal conductivity k. The thermal resistance of the cylinder for radial conduction is

1. 1. In(r2/r1)

      2πkL

   
   
   

   2. In(r2/r1)

      2πkL

   
   
   

   3. 2πkL

      In(r2/r1)

   
   
   

   4. 2πkL

      In(r1/r2)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   In(r2/r1)

   2πkL

   Correct Option: A

   In(r2/r1)

   2πkL

---

79. For flow of viscous fluid over a flat plate, if the fluid temperature is the same as the plate temperature, the thermal boundary layer is

1. 1. thinner than the velocity boundary layer

   
   
   

   2. thicker than the velocity boundary layer

   
   
   

   3. of the same thickness as the velocity boundary layer

   
   
   

   4. not formed at all

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: D

   NA

---

---

80. An industrial gas (c = 1 kJ/kgK) enters a parallel flow heat exchange at 250°C with a flow rate of 2 kg/s to heat a water stream. The water stream (c = 4 kJ/kgK) enters the heat exchange at 50°C with a flow rate of 1 kg/s. The heat exchange has an effectiveness of 0.75. The gas stream exit temperature will be

1. 1. 75°C

   
   
   

   2. 100°C

   
   
   

   3. 125°C

   
   
   

   4. 150°C

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   

   ε =	Ch(Th1 - Th2)
   	Cmin(Thi - Tci)

   
   

   0.75 =	2 ×(250 - Th2)
   	2 ×(250 - 50)

   
   T_h2 = 100° C

   Correct Option: B

   
   

   ε =	Ch(Th1 - Th2)
   	Cmin(Thi - Tci)

   
   

   0.75 =	2 ×(250 - Th2)
   	2 ×(250 - 50)

   
   T_h2 = 100° C

---