Heat Transfer Miscellaneous

Heat Transfer Miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Heat-Transfer

Heat Transfer Miscellaneous
  1. The ratios of the laminar hydrodynamic boundary layer thickness to thermal boundary layer thickness of flows of two fluids P and Q on a flat plate are 1/2 and 2 respectively. The Reynolds number based on the plate length for both the flows is 104. The Prandtl and Nusselt numbers for P are 1/8 and 35 respectively. The Prandlt and Nusselt numbers for Q are respectively








  1. View Hint View Answer Discuss in Forum

    δt
    		=
    1
    		× Pr-1/3
    δ1.026

    For fluid Q: 1/2 =
    δt
    		=
    1
    		× Pr-1/3
    δ1.026

    ⇒ Pr = 8
    For fluid P: Laminar flow over flat plate Nu = 0.664 ReL1/2 Pr1/3 = 35
    Similarly for fluid Q: Nu = 0.664 ReL1/2 Pr1/3
    = 0.664 (104)1/2 81/3 ≃ 140

    Correct Option: A

    δt
    		=
    1
    		× Pr-1/3
    δ1.026

    For fluid Q: 1/2 =
    δt
    		=
    1
    		× Pr-1/3
    δ1.026

    ⇒ Pr = 8
    For fluid P: Laminar flow over flat plate Nu = 0.664 ReL1/2 Pr1/3 = 35
    Similarly for fluid Q: Nu = 0.664 ReL1/2 Pr1/3
    = 0.664 (104)1/2 81/3 ≃ 140

  1. The total e-missive power of a surface is 500 W/ m2 at temperature T1 and 1200 W/m2 at temperature T2, where the temperature are in Kelvin. Assuming the e-missivity of the surface to be constant, the ratio of the temperature T1 /T2 is








  1. View Hint View Answer Discuss in Forum

    E-missive power ∝ T4

    ⇒
    500
    		=
    T1
    		4
    1200T2

    ∴
    T1
    		= 0.8034
    T2

    Correct Option: C

    E-missive power ∝ T4

    ⇒
    500
    		=
    T1
    		4
    1200T2

    ∴
    T1
    		= 0.8034
    T2

  1. An infinitely long function 0.5 m × 0.4 m cross section is shown in the figure below. Consider all surfaces of the furnace to be black. The top and bottom walls are maintained at temperature T1 = T3 = 927°C while the side walls are attemperature T2 = T4 = 527°C. The view factor, F1 - 2 is 0.26.The net radiation heat loss or gain on side 1 is ______ W/m.
    Stefan-Boltzmann constant = 5.67 × 10-8 W/ m2K4.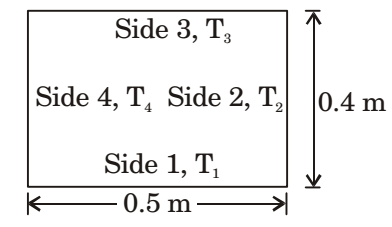








  1. View Hint View Answer Discuss in Forum

    T1 = 927°C = 1200 K,
    T2 = 527°C = 800 K,
    F12 = F14 = 0.26
    F11 + F12 + F13 + F14 = 1
    F13 = 0.48
    Q = Q12 + Q13 + Q14
    Q13 = 0 since the temperatures are same
    Q = Q12 + Q14 = 2 × σb × A × F12 ×(T14 - T24)
    Q = 2 × 5.67 × 10-8 × (0.5 × 1) × 0.26 × (12004 – 8004)
    = 24530.688

    Correct Option: A

    T1 = 927°C = 1200 K,
    T2 = 527°C = 800 K,
    F12 = F14 = 0.26
    F11 + F12 + F13 + F14 = 1
    F13 = 0.48
    Q = Q12 + Q13 + Q14
    Q13 = 0 since the temperatures are same
    Q = Q12 + Q14 = 2 × σb × A × F12 ×(T14 - T24)
    Q = 2 × 5.67 × 10-8 × (0.5 × 1) × 0.26 × (12004 – 8004)
    = 24530.688

  1. Two large parallel plates having a gap of 10 mm in between them are maintained at temperatures T1, = 1000 K and T2 = 400 K. Given emissivity values, ε1 = 0.5, ε2 = 0.25 and Stefan-Boltzmann constant σ = 5.67 × 10-8 W/ m2K4, the heat transfer between the plates (in kW/m2) is ______








  1. View Hint View Answer Discuss in Forum


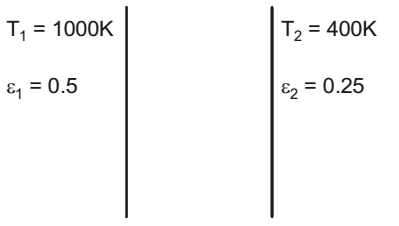
    Q + 2 =
    σ(T14 - T24)
    1
    		+
    1
    		- 1
    ε1ε2

    =
    5.76 ×10-8(10004 - 4004)
    1
    		+
    1
    		- 1
    0.50.25

    = 11049.696 W/m2
    = 11.049 kW/m2

    Correct Option: A


    Q + 2 =
    σ(T14 - T24)
    1
    		+
    1
    		- 1
    ε1ε2

    =
    5.76 ×10-8(10004 - 4004)
    1
    		+
    1
    		- 1
    0.50.25

    = 11049.696 W/m2
    = 11.049 kW/m2

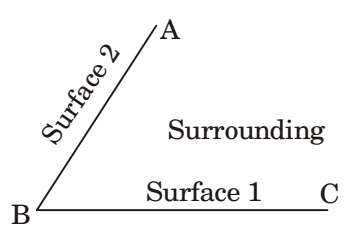
  1. Two black surfaces, AB and BC, of length 5m and 6 m, respectively, are oriented as shown. Both surfaces extend infinitely into the third dimension. Given that view factor F12 = 0.5. T1 = 800 K, T2 = 600 K, Tsurrounding = 300 K and Stefan Boltzmann constant, a = 5.67 × 10-8 W/ (m2K4), the heat transfer rate from Surface 2 to the surrounding environment is _____kW.








  1. View Hint View Answer Discuss in Forum

    F12 = 0.5

    T1 = 800 K, T2 = 600 K
    Tsurrounding = 300 K
    Let (3) denote the surrounding environment (Assume unit width perpendicular to plane of Fig.)
    From summation rule:
    F21 + F22 + F23 = 1
    F21 + F23 = 1
    ∴ F22 = 0
    or F23 = 1 – F21
    A1 F12 = A2 F21 = 6 × 1 × 0.5
    = (5 × 1) × F21

    F21 =
    6 × 0.5
    		= 0.6
    5

    ∴ F23 = 1 – F21 = 0.4
    Since surrounding environment being large. No surface has a surface resistance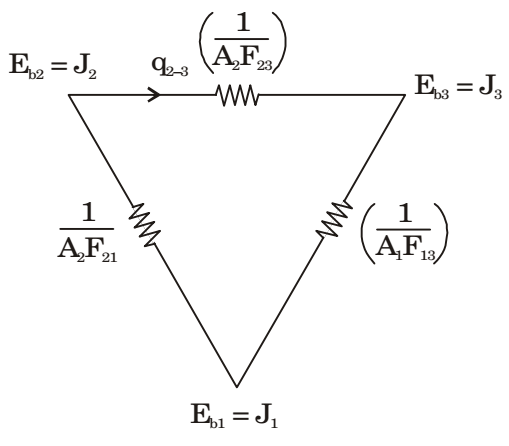

    Heat transfer rate from (2) and (3)
    =
    Eb2 - Eb3
    1
    A2F23

    =
    σ(T24 - T34)
    1
    A2F23

    =
    10-8(6004 - 3004)
    1
    5 × 1 × 0.4

    = 13.778 kW/metre
    Assume that heat exchange is per unit width perpendicular to plane of figure.

    Correct Option: C

    F12 = 0.5

    T1 = 800 K, T2 = 600 K
    Tsurrounding = 300 K
    Let (3) denote the surrounding environment (Assume unit width perpendicular to plane of Fig.)
    From summation rule:
    F21 + F22 + F23 = 1
    F21 + F23 = 1
    ∴ F22 = 0
    or F23 = 1 – F21
    A1 F12 = A2 F21 = 6 × 1 × 0.5
    = (5 × 1) × F21

    F21 =
    6 × 0.5
    		= 0.6
    5

    ∴ F23 = 1 – F21 = 0.4
    Since surrounding environment being large. No surface has a surface resistance

    Heat transfer rate from (2) and (3)
    =
    Eb2 - Eb3
    1
    A2F23

    =
    σ(T24 - T34)
    1
    A2F23

    =
    10-8(6004 - 3004)
    1
    5 × 1 × 0.4

    = 13.778 kW/metre
    Assume that heat exchange is per unit width perpendicular to plane of figure.