Heat Transfer Miscellaneous
- Steam in the condenser of a thermal power plant is to be condensed at a temperature of 30°C with cooling water which enters the tubes of the condenser at 14°C and exits at 22°C. The total surface area of the tubes is 50 m2, and the overall heat transfer coefficient is 2000 W/ m2. The heat transfer (in MW) to the condenser is ______(correct to two decimal places).
-
View Hint View Answer Discuss in Forum
Condenser is given.
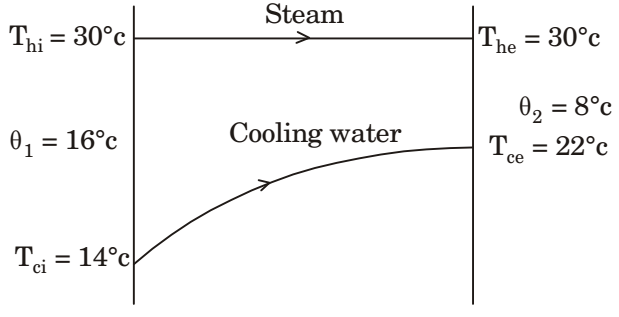
LMTD = θ1 - θ2 In 
θ1 
θ2 = 16 - 8 = 11.54°C In 
16 
8
Q = UA (LMTD)
= 2000 × 50 × 11.54 = 1.154 MWCorrect Option: A
Condenser is given.

LMTD = θ1 - θ2 In 
θ1 
θ2 = 16 - 8 = 11.54°C In 
16 
8
Q = UA (LMTD)
= 2000 × 50 × 11.54 = 1.154 MW
- Air enters a counter flow HE at 70°C and leaves at 40°C. Water enters at 30°C and leaves at 50°C, the LMTD in degree C is
-
View Hint View Answer Discuss in Forum
∴ ∆T1 = 70 – 50 = 20°C, ∆T2 = 40 – 30 = 10°C
LMTD = ∆T1 ∆T2 log 
∆T1 
∆T2 = 20 - 10 = 14.43 log 
20 
10 Correct Option: B
∴ ∆T1 = 70 – 50 = 20°C, ∆T2 = 40 – 30 = 10°C
LMTD = ∆T1 ∆T2 log 
∆T1 
∆T2 = 20 - 10 = 14.43 log 
20 
10
- The value of Biot number is very small (less than 0.01),when
-
View Hint View Answer Discuss in Forum
When conductive resistance of solid is negligible, then biot number is very small.
Correct Option: C
When conductive resistance of solid is negligible, then biot number is very small.
- A spherical thermocouple junction of diameter 0.706 mm is to be used for the measurement of temperature of a gas stream. The convective heat transfer coefficient on bead surface is 400 W/m2K, Thermophysical properties of thermocouple material are k = 20 W/mK, c = 400 J/kgK and ρ = 8500 kg/m3. If the thermocouple initially at 30°C is placed in a hot stream of 300°C, the time taken by the bead to reach 298°C, is
-
View Hint View Answer Discuss in Forum
Given h = 400 W/m2K, k = 20 W/mK
c = 400 J/kg.K, ρ = 8500 kg/m3 T(t) = 298 °C, Ti = 30 °C, T∞ = 300 °CL = V = (π / 6)D3 = D A πD2 6 = 1 × 0.706 × 10-3 = 1.76 × 10-4 m 6 Biot Number = hL k = 400 × 1.176 × 10-4 = 0.0023 20
Since Bi < 0.1, lumped system analysis can be used
T(t) = e -hAT Ti - T∞ ρcv 298 - 300 = e -hAT 30 - 300 ρcV -2 = e -hAT 270 ρcV ln 
270 
= hAT 2 ρcV ⇒ T = ρcV ln 
270 
= ρc 
V 
ln 135 cA 2 h A = 8500 × 400 × 1.176 × 10-4 × 4.90 ≈ 4.9 sec. 400 Correct Option: B
Given h = 400 W/m2K, k = 20 W/mK
c = 400 J/kg.K, ρ = 8500 kg/m3 T(t) = 298 °C, Ti = 30 °C, T∞ = 300 °CL = V = (π / 6)D3 = D A πD2 6 = 1 × 0.706 × 10-3 = 1.76 × 10-4 m 6 Biot Number = hL k = 400 × 1.176 × 10-4 = 0.0023 20
Since Bi < 0.1, lumped system analysis can be used
T(t) = e -hAT Ti - T∞ ρcv 298 - 300 = e -hAT 30 - 300 ρcV -2 = e -hAT 270 ρcV ln 
270 
= hAT 2 ρcV ⇒ T = ρcV ln 
270 
= ρc 
V 
ln 135 cA 2 h A = 8500 × 400 × 1.176 × 10-4 × 4.90 ≈ 4.9 sec. 400
- A small copper ball of 5 mm diameter at 500 K is dropped into an oil bath whose temperature is 300 K. The thermal conductivity of copper is 400 W/mK, its density 9000 kg/m3 and its specific heat 385 J/kgK. If the heat transfer coefficient is 250 W/m2K and lumped analysis is assumed to be valid, the rate of fall of the temperature of the ball at the beginning of cooling will be, in K/s,
-
View Hint View Answer Discuss in Forum
Given data: K = 400 W/mK; Ti = 500 K ; ρ = 9000 Kg/m3.
T∞ = 300 K; Cp = 385 J/KG K; h = 250 W /m2KLc = V = D = (0.005) = 8.33 × 10-4 A 6 6 T = T∞ + (Ti - T∞) e -hAT ρcV dT = -hAT (Ti - T∞) e -hAT dt ρcV ρcV 
dT 
= hA (Ti - T∞) dt t = 0 ρcV = 250 × 200 = 17.31 K / S 9000 × 385 × 8.33 × 10-4 Correct Option: C
Given data: K = 400 W/mK; Ti = 500 K ; ρ = 9000 Kg/m3.
T∞ = 300 K; Cp = 385 J/KG K; h = 250 W /m2KLc = V = D = (0.005) = 8.33 × 10-4 A 6 6 T = T∞ + (Ti - T∞) e -hAT ρcV dT = -hAT (Ti - T∞) e -hAT dt ρcV ρcV 
dT 
= hA (Ti - T∞) dt t = 0 ρcV = 250 × 200 = 17.31 K / S 9000 × 385 × 8.33 × 10-4

