Heat Transfer Miscellaneous Easy Questions and Answers | Page - 7

Heat Transfer Miscellaneous

Which one of the following configurations has the highest fin effectiveness?

1. Thin, closely spaced fins
1. Thin, widely spaced fins
1. Thick, widely spaced fins
1. Thick, closely spaced fins

View Hint View Answer Discuss in Forum

NA

Correct Option: A

NA

The heat loss from a fin is 6 W. The effectiveness and efficiency of the fin are 3 and 0.75 respectively. The heat loss (in W) from the fin, keeping the entire fin surface at base temperature is _____.

1. 10 W
1. 8 W
1. 18 W
1. 16 W

View Hint View Answer Discuss in Forum

η_fin = q_actual
q_{maximum possible}

q_max = 6 = 8 W
0.75

Correct Option: B

η_fin = q_actual
q_{maximum possible}

q_max = 6 = 8 W
0.75

A solid sphere of radius r₁ = 20 mm is placed concentrically inside a hollow sphere of radius r₂ = 30 mm as shown in the figure.

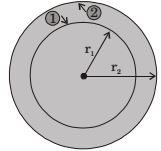
The view factor F₂₁ for radiation heat transfer is

1. 2
  3
1. 4
  9
1. 8
  27
1. 9
  4

View Hint View Answer Discuss in Forum

F₁₁ + F₁₂ = 1, here F₁₁ = 0
∴ F₁₂ = 1

Now from reciprocating law
A₁ F₁₂ = A₂ F₂₁
∴ 22π (20)² × 1 = 2π (30)² × F₂₁
⇒ F₂₁ = 10 ² = 4
30 9

Correct Option: B

F₁₁ + F₁₂ = 1, here F₁₁ = 0
∴ F₁₂ = 1

Now from reciprocating law
A₁ F₁₂ = A₂ F₂₁
∴ 22π (20)² × 1 = 2π (30)² × F₂₁
⇒ F₂₁ = 10 ² = 4
30 9

Three sets of parallel plates LM, NR and PQ are given in Figures 1, 2 and 3. The view factor Fij is defined as the fraction of radiation leaving plate I that is intercepted by plate J. Assume that the val ues of FL M and FN R ar e 0.8 and 0.4, respectively. The value of FPQ (round off to one decimal place) is _____.

1. 1.6
1. 0.6
1. 1.9
1. 0.16

View Hint View Answer Discuss in Forum

F_LM = F(I) + F(II) + F(III)
Where F is shape factor of surface area I, II and III of M with surface area of ‘L’
0.8 = F(I) + F(II) + F(III)
∵ (I) and (III) are symmetrical in shape so, shape factor of these surface will be same i.e. F(I) = F(III)
So, 0.8 = 2F(I) + F(II)... (1)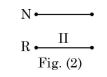

In this area (II) is same as fig. (I) area II.
i.e. F_NR = F(II) = 0.4... (2)
From equation (1),
F(III) = 0.8 - 0.4 = 0.2
2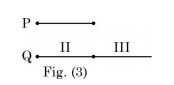

Here, F_PQ = F(II) + F(III)
= 0.4 + 0.2 = 0.6

Correct Option: B

F_LM = F(I) + F(II) + F(III)
Where F is shape factor of surface area I, II and III of M with surface area of ‘L’
0.8 = F(I) + F(II) + F(III)
∵ (I) and (III) are symmetrical in shape so, shape factor of these surface will be same i.e. F(I) = F(III)
So, 0.8 = 2F(I) + F(II)... (1)

In this area (II) is same as fig. (I) area II.
i.e. F_NR = F(II) = 0.4... (2)
From equation (1),
F(III) = 0.8 - 0.4 = 0.2
2

Here, F_PQ = F(II) + F(III)
= 0.4 + 0.2 = 0.6

For flow of fluid over a heated plate, the following fluid properties are known: viscosity = 0.001 Pa.s; specific heat at constant pressure = 1 kJ/kgK; thermal conductivity = 1 W/mK. The hydrodynamic boundary layer thickness at a specified location on the plate is 1 mm. The thermal boundary layer thickness at the same location is

1. 0.001 mm
1. 0.01 mm
1. 1 mm
1. 1000 mm

View Hint View Answer Discuss in Forum

Given:
µ =0.001 Pa – s
C_P = 1 kJ/kg K
K_f = 1W/mK (Fluid thermal conductivity)
Hydrodynamic boundary layer thickness, δ = 1 mm
P_r = μC_P = 0.001 × 1000 = 1
K_f 1

δ _t = δ (C_r)^-1/3
= 1 × (1)^-1/3 = 1 mm

Correct Option: C

Given:
µ =0.001 Pa – s
C_P = 1 kJ/kg K
K_f = 1W/mK (Fluid thermal conductivity)
Hydrodynamic boundary layer thickness, δ = 1 mm
P_r = μC_P = 0.001 × 1000 = 1
K_f 1

δ _t = δ (C_r)^-1/3
= 1 × (1)^-1/3 = 1 mm