-
An isosceles triangle ABC is rightangled at B.D is a point inside the triangle ABC. P and Q are the feet of the perpendiculars drawn from D on the side AB and AC respectively of ∆ ABC. If AP = a cm, AQ = b cm and ∠BAD = 15°, sin 75°=
-
-
2b √3a -
a 2b -
√3a 2b -
2a √3b
-
Correct Option: C
As per the given in question , we draw a figure of an isosceles triangle ABC 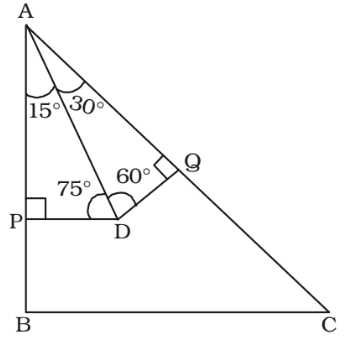
From ∆ AQD,
| sin 60° = | |
| AD |
| ⇒ | = | ||
| 2 | AD |
| ⇒ AD = | |
| √3 |
From ∆ APD,
| sin 75° = | = | = | |||
| AD | 2b | ||||
| √3 |

