-
Two posts are x meter apart and the height of one is double that of the other. If from the midpoint of the line joining their feet, an observer finds the angular elevations of their tops to be complementary, then the height (in meter) of the shorter post is :
-
-
x 2 √2 -
x 4 - x √2
-
x √2
-
Correct Option: A
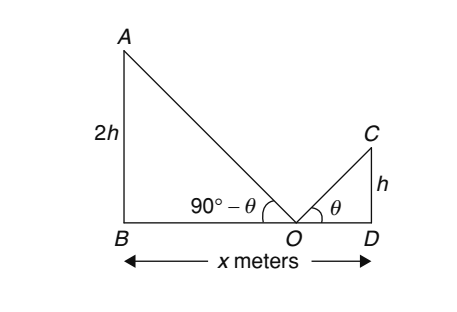
Let us draw the figure from the given question.
In figure , CD = h m, AB = 2h m
| OB = OD | = | x | m | 2 |
| From ΔOCD, |
| tan θ | = | h | = | 2h | .......( 1 ) |
| x | |||||
| 2 |
| From ΔOAB, |
| tan( 90° - θ ) | = | AB | BO |
| ⇒ cot θ | = | 2h | = | 4h | ......( 2 ) |
| x | |||||
| 2 |
| Multiplying both equations ( 1 ) and ( 2 ) , |
| tanθ cot θ | = | 2h | × | 4h |
| ⇒ | x 2 = 8h2 |
| ⇒ | h2 = | 8 |
| ⇒ | h = | m | 2√2 |
| Hence, the height of the shorter post is | x | m |