256. The black box in the figure consists of a minimum complexity circuit that uses only AND, OR and NOT gates. The function f(x, y, z) = 1 whenever x, y are different and 0 otherwise. In addition the 3 inputs x, y, z are never all the same value. Which one of the following equations leads to the correct design for the minimum complexity circuit?
     
     
     
     

1. 1. x' y + xy'
      

   
   
   

   2. x + y'z
      

   
   
   

   3. x'y'z' + xy'z
      

   
   
   

   4. xy + y'z + z'

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: A

   NA

---

257. Consider the following statements:
     1. Minimization using Karnaugh map may not provide unique solution.
     2. Redundant grouping in Karnaugh map may result in non-minimized solution.
     3. Don't care states of used in Karnaugh map for minimization, the minimal solution is not obtained.
     Which of the statements given above are correct?
     

1. 1. 1, 2 and 3
      

   
   
   

   2. 2 and 3 only
      

   
   
   

   3. 1 and 3 only
      

   
   
   

   4. 1 and 2 only

   
   
   

---

1. View Hint View Answer Discuss in Forum

   With reference to K-map
   ● Minimization using Karnaugh map may not provide unique solution
   ● Redundant grouping in Karnaugh map may result in non-minimized solution.

   Correct Option: D

   With reference to K-map
   ● Minimization using Karnaugh map may not provide unique solution
   ● Redundant grouping in Karnaugh map may result in non-minimized solution.

---

---

258. What is the Boolean expression for the truth table shown below?
     
     
     

1. 1. B (A + C) (A + C)

   
   
   

   2. B (A +C) ( A+ C)

   
   
   

   3. B( A + B (A + C) (A + C)

   
   
   

   4. B (A + C) (A + + C)

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: A

   NA

---

259. Consider the following statements:
     For 3 input variables a, b, c; a Boolean function y = ab + bc + ca represents:
     1. a 3-input majority gate
     2. a 3-input minority gate
     3. Carry output of a full adder
     4. Product circuit for a, b and c
     Which of the above statements are correct?

1. 1. 1 and 4 only
      

   
   
   

   2. 2 and 3 only
      

   
   
   

   3. 1 and 3 only
      

   
   
   

   4. 3 and 4 only

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: C

   NA

---

---

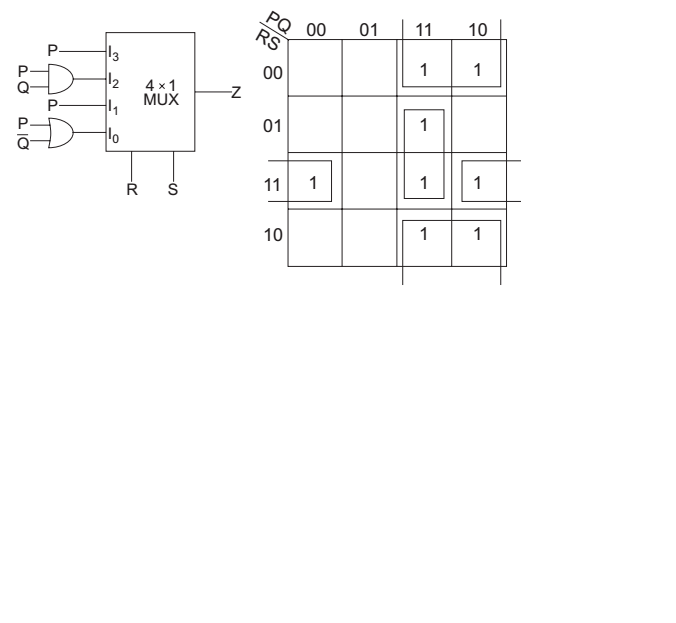
260. For the circuit shown in the following figure, I0 – I3 are inputs to the 4: 1 multiplexer, R (MSB) and P and Q are control bits. The output Z can be represented by—
     
     
     

1. 1. PS+ P Q S + R S Q

   
   
   

   2. P Q + PQR + P Q S

   
   
   

   3. P Q R + PQR + PQ R S + Q R S

   
   
   

   4. PQR+ PQRS + PQ RS + Q R S

   
   
   

---

1. View Hint View Answer Discuss in Forum

   The given circuit
   Z = + R + SP + + RSPQ + R + SP + RS (P + + Q)
   or
   Z = + R + SP + + RSPQ + PR + S + PRS + + QRS
   From above K-map, we get
   Z=P + S + PQS + RS + Q

   
   

   Correct Option: A

   The given circuit
   Z = + R + SP + + RSPQ + R + SP + RS (P + + Q)
   or
   Z = + R + SP + + RSPQ + PR + S + PRS + + QRS
   From above K-map, we get
   Z=P + S + PQS + RS + Q

   
   

---