Digital electronics miscellaneous

Digital electronics miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Digital Electronics

Digital electronics miscellaneous
  1. The octal equivalent of the HEX number AB. CD is—








  1. View Hint View Answer Discuss in Forum

    NA

    Correct Option: B

    NA

  1. The addition of two binary variables A and B results into a SUM and a CARRY output. Consider the following expressions for the SUM and CARRY outputs—








  1. View Hint View Answer Discuss in Forum

    SUM = A ⊕ B = A B + BA
    CARRY = AB

    Correct Option: B

    SUM = A ⊕ B = A B + BA
    CARRY = AB

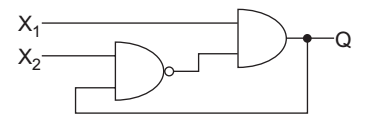
  1. In the figure, as long as X1 = 1 and X2 = 1, the output Q remains—










  1. View Hint View Answer Discuss in Forum

    As long as X1 = 1 and X2 = 1
    Since the output is feedback to input NAND gate. It means output is toggle between 0 → 1 → 0 → 1…… makes the output Q unstable.


    Correct Option: D

    As long as X1 = 1 and X2 = 1
    Since the output is feedback to input NAND gate. It means output is toggle between 0 → 1 → 0 → 1…… makes the output Q unstable.


  1. A digital circuit which compares two numbers A3 A2A1 A0 and B3 B2 B1 B0 is shown below. To get the output
    X = 0, choose one pair of correct input numbers—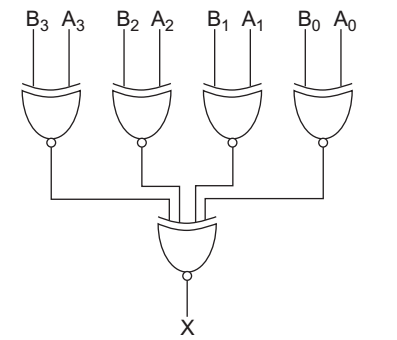










  1. View Hint View Answer Discuss in Forum

    To get the output zero i.e., X = 0.
    Applying hit and trial method in order to choose the pair of number.
    (A) For input 1 0 1 0, 1 0 1 0 output
    Y1 = 0, Y2 = 0, Y3 = 0, Y4 = 0
    Now, X = Y1 Y2 Y3 Y4 + Y1 Y2 Y3 Y4
    or X = 0. 0. 0. 0 + 0 0 0 0 = 1 (Not required)
    (B) For input 0 1 0 1, 0 1 0 1 output
    Y1 = 0, Y2 = 0, Y3 = 0, Y4 = 0
    Now, X = Y1 Y2 Y3 Y4 + Y1 Y2 Y3 Y4
    or X = 0. 0. 0. 0 + 0 0 0 0 = 1 (Not required)
    (C) For input 0 0 1 0, 0 0 1 0 output
    Y1 = 0, Y2 = 0, Y3 = 0, Y4 = 0
    Now, X = Y1 Y2 Y3 Y4 + Y1 Y2 Y3 Y4
    or X = 0. 0. 0. 0 + 0 0 0 0 = 1 (Not required)
    (D) For input 1 0 1 0, 1 0 1 1 output
    Y1 = 0, Y2 = 0, Y3 = 0, Y4 = 0
    Now, X = Y1 Y2 Y3 Y4 + Y1 Y2 Y3 Y4
    or X = 0. 0. 0. 0 + 0 0 0 1 = 0 + 0 = 0
    This is required condition. Hence alternative (D) is the correct choice.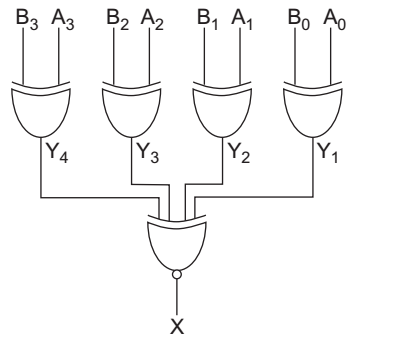


    Correct Option: D

    To get the output zero i.e., X = 0.
    Applying hit and trial method in order to choose the pair of number.
    (A) For input 1 0 1 0, 1 0 1 0 output
    Y1 = 0, Y2 = 0, Y3 = 0, Y4 = 0
    Now, X = Y1 Y2 Y3 Y4 + Y1 Y2 Y3 Y4
    or X = 0. 0. 0. 0 + 0 0 0 0 = 1 (Not required)
    (B) For input 0 1 0 1, 0 1 0 1 output
    Y1 = 0, Y2 = 0, Y3 = 0, Y4 = 0
    Now, X = Y1 Y2 Y3 Y4 + Y1 Y2 Y3 Y4
    or X = 0. 0. 0. 0 + 0 0 0 0 = 1 (Not required)
    (C) For input 0 0 1 0, 0 0 1 0 output
    Y1 = 0, Y2 = 0, Y3 = 0, Y4 = 0
    Now, X = Y1 Y2 Y3 Y4 + Y1 Y2 Y3 Y4
    or X = 0. 0. 0. 0 + 0 0 0 0 = 1 (Not required)
    (D) For input 1 0 1 0, 1 0 1 1 output
    Y1 = 0, Y2 = 0, Y3 = 0, Y4 = 0
    Now, X = Y1 Y2 Y3 Y4 + Y1 Y2 Y3 Y4
    or X = 0. 0. 0. 0 + 0 0 0 1 = 0 + 0 = 0
    This is required condition. Hence alternative (D) is the correct choice.


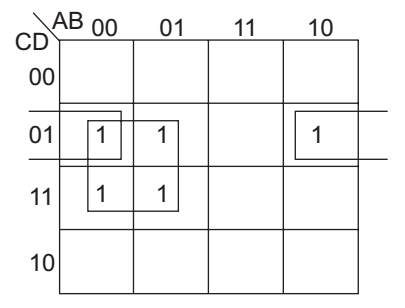
  1. The simplified form of the Boolean expression Y = ( ABC + D) ( AD + B C) can be written as—








  1. View Hint View Answer Discuss in Forum

    Given expression
    Y = (ABC + D) (AD + B C)
    or Y = ABCAD + DA D + ABC B C + D B C
    or Y = ABCD + A D + DB C
    Now, further it can be easily solved by using K-map.
    Now, from K-map, we get
    Y = AD + B CD.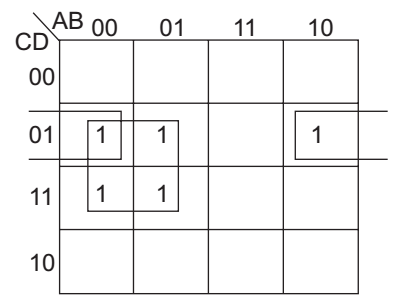


    Correct Option: A

    Given expression
    Y = (ABC + D) (AD + B C)
    or Y = ABCAD + DA D + ABC B C + D B C
    or Y = ABCD + A D + DB C
    Now, further it can be easily solved by using K-map.
    Now, from K-map, we get
    Y = AD + B CD.