Digital electronics miscellaneous

Digital electronics miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Digital Electronics

Digital electronics miscellaneous
  1. Consider the following logic circuit. What is the required input condition (A, B, C) to make the output X = 1?










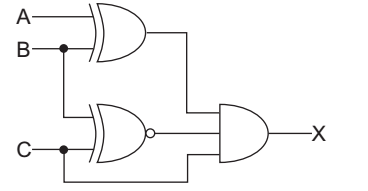
  1. View Hint View Answer Discuss in Forum

    To get X = 1 output of EX-OR gate and EX - NOR gate must be 1 and in order to make
    Y1 = 1 → A should be 0 and B should be 1
    Y2 = 1 → C should be 1 and B should be 1. So, to
    get X = 1 the condition (0, 1, 1) is correct.


    Correct Option: D

    To get X = 1 output of EX-OR gate and EX - NOR gate must be 1 and in order to make
    Y1 = 1 → A should be 0 and B should be 1
    Y2 = 1 → C should be 1 and B should be 1. So, to
    get X = 1 the condition (0, 1, 1) is correct.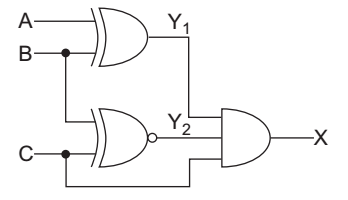


  1. In Boolean algebra if F = (A + B) ( A + C), then—








  1. View Hint View Answer Discuss in Forum

    Given, F = (A + B) ( A + C)
    or F = AA + AB + BC + AC
    or F = AB + BC + AC
    To minimize this function, it can be solved easily by using K-map given below:
    From K-map, we get F = AB + AC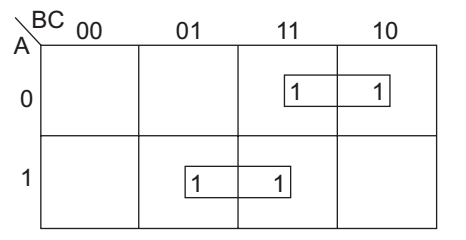


    Correct Option: C

    Given, F = (A + B) ( A + C)
    or F = AA + AB + BC + AC
    or F = AB + BC + AC
    To minimize this function, it can be solved easily by using K-map given below:
    From K-map, we get F = AB + AC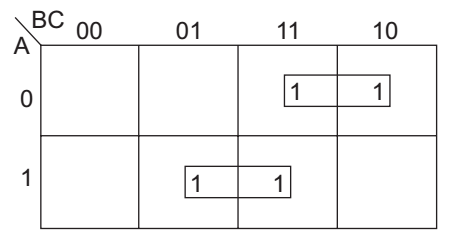


  1. To add two m-bit numbers, the required number of half adder is—








  1. View Hint View Answer Discuss in Forum

    To add two m-bit numbers, the required no. of half adder is 2m–1.

    Correct Option: A

    To add two m-bit numbers, the required no. of half adder is 2m–1.

  1. When signed numbers are used in binary arithmetic, then which one of the following notations would have unique representation for zero?








  1. View Hint View Answer Discuss in Forum

    When signed numbers are used in binary arithmetic, then 2’S complement notation would have unique representation for zero.

    Correct Option: C

    When signed numbers are used in binary arithmetic, then 2’S complement notation would have unique representation for zero.

  1. The addition of two binary variables A and B results into a SUM and a CARRY output. Consider the following expressions for the SUM and CARRY outputs—








  1. View Hint View Answer Discuss in Forum

    SUM = A ⊕ B = A B + BA
    CARRY = AB

    Correct Option: B

    SUM = A ⊕ B = A B + BA
    CARRY = AB