Digital electronics miscellaneous

Digital electronics miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Digital Electronics

Digital electronics miscellaneous
  1. In Boolean algebra if F = (A + B). ( A + C), then—








  1. View Hint View Answer Discuss in Forum

    NA

    Correct Option: C

    NA

  1. Which one of the following statement is correct? For a 4- input NOR gate, when only two inputs are to be used, the best option for the used input is to—








  1. View Hint View Answer Discuss in Forum

    The given four inputs NOR gate
    When only two inputs are used then rest inputs must be connected to ground, because if any input is connected to Vcc we will get output 0 irrespective of the applied input. However if inputs are open we get floating output. Hence option (A) is the best choice.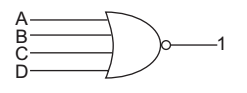


    Correct Option: A

    The given four inputs NOR gate
    When only two inputs are used then rest inputs must be connected to ground, because if any input is connected to Vcc we will get output 0 irrespective of the applied input. However if inputs are open we get floating output. Hence option (A) is the best choice.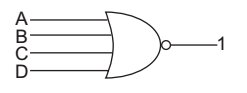


  1. Minimum no. of NAND gates require to implement the logic Y = AB + A + B + C








  1. View Hint View Answer Discuss in Forum

    Given Y = AB + A + B + C
    or Y = A + B + A + B C
    or Y = 1 + B + B C
    or Y = 1
    Therefore, no NAND gates required to implement the logic.

    Correct Option: A

    Given Y = AB + A + B + C
    or Y = A + B + A + B C
    or Y = 1 + B + B C
    or Y = 1
    Therefore, no NAND gates required to implement the logic.

  1. Which the Boolean function
    F (X1, X2, X3) = Σ(0,1, 2, 3) + ∑d (4, 5, 6, 7) is minimized?








  1. View Hint View Answer Discuss in Forum

    Given, F (X1, X2, X3) = Σ(0,1, 2, 3) + ∑d (4, 5, 6, 7)
    From K-map, we get F (X1, X2, X3 )= 1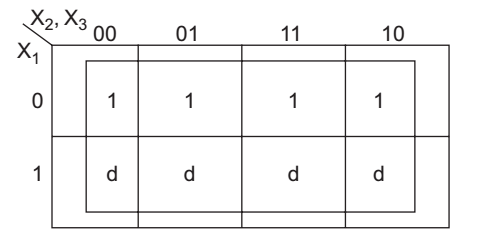


    Correct Option: A

    Given, F (X1, X2, X3) = Σ(0,1, 2, 3) + ∑d (4, 5, 6, 7)
    From K-map, we get F (X1, X2, X3 )= 1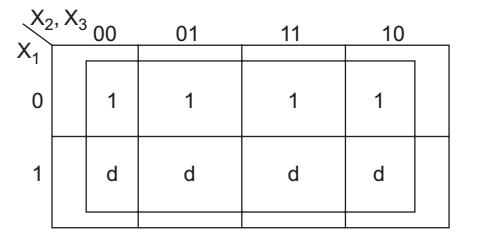


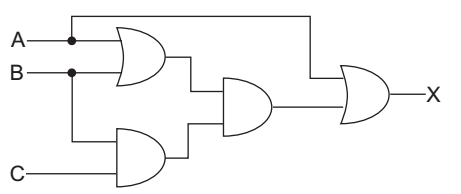
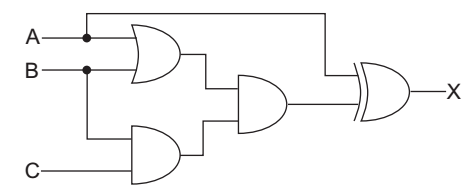
  1. For the logic circuit given. Which is the simplified Boolean function?










  1. View Hint View Answer Discuss in Forum

    X = A + (A + B) (C + B)
    or X = A + AC + BC + AB + B
    or X = A (1 + C) + BC + B (A + 1)
    or X = A + BC + B
    or X = A + B (1 + C)
    or X = A + B [Since 1 + C = 1]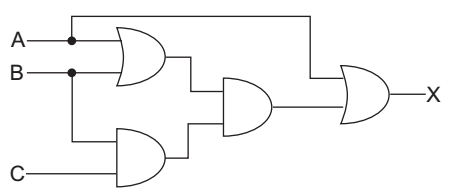


    Correct Option: B

    X = A + (A + B) (C + B)
    or X = A + AC + BC + AB + B
    or X = A (1 + C) + BC + B (A + 1)
    or X = A + BC + B
    or X = A + B (1 + C)
    or X = A + B [Since 1 + C = 1]