-
An aeroplane when flying at a height of 5000 m from the ground passes vertically above another aeroplane at an instant, when the angles of elevation of the two aeroplanes from the same point on the ground are 60° and 45° respectively. The vertical distance between the aeroplanes at that instant is
-
- 5000 (√3 - 1 ) m
- 5000 (3 - √3 ) m
-
5000 
1 - 1 
m √3 - 4500 m
Correct Option: C
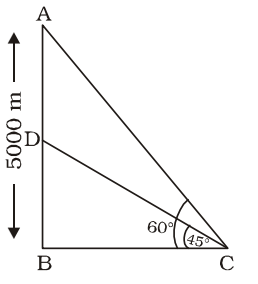
∠ACB = 60°
∠DCB = 45°
AB = 5000 metre
AD = x metre
∴ From ∆ABC,
| tan 60° = | BC |
| ⇒ √3 = | BC |
| ⇒ BC = | metre | √3 |
From ∆DBC,
| tan45° = | BC |
| ⇒ DB = BC = | √3 |
∴ AD = AB – BD
| = 5000 - | √3 |
| 5000 |  | 1 - |  | m | √3 |

