-
An observer on the top of a mountain, 500 m above the sea level, observes the angles of depression of the two boats in his same place of vision to be 45° and 30° respectively. Then the distance between the boats, if the boats are on the same side of the mountain, is
-
- 456 m
- 584 m
- 366 m
- 699 m
Correct Option: C
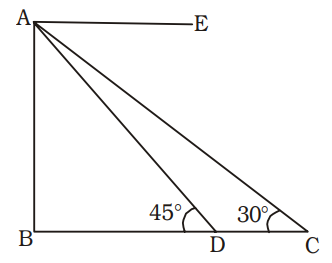
AB = Height of mountain = 500 metre
∠ACB = 30° ; ∠ADB = 45°
C and D ⇒ Positions of boats
Let CD = x metre
From ∆ ABD,
| tan 45° = | BD |
⇒ AB = BD
= 500 metre
From ∆ ABC,
| tan 30° = | BC |
| ⇒ | = | √3 | 500 + x |
⇒ 500 + x = 500 √3
⇒ x = 500 √3 – 500
= 500 (√AAA - 1) metre
= 500 (1.732 – 1) metre
= (500 × 0.732) metre
= 366 metre

