The angle of elevation of the top of a pillar from the foot

Home » Aptitude » Trigonometry » Question

The angle of elevation of the top of a pillar from the foot and the top of a building 20 m high, are 60° and 30° respectively. The height of the pillar is

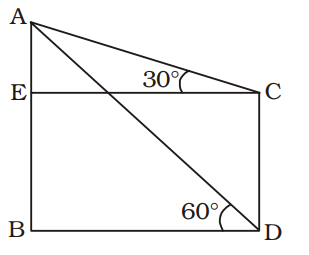
Let, AB = height of pole = h metre
CD = height of building = 20 metre = BE
∠ADB = 60° ; ∠ACE = 30°
Let, AE = x metre ; BD = EC = y metre
In ∆ ABD,

tan 60° =		AB	⇒ √3 =	x + 20
		BD		y

⇒ x + 20 = √3 y .... (i)
In ∆ AEC

tan 30° =	AE
	EC

⇒		1	=	x	⇒ y = √3 x ....(ii)
		√3		y

From equation (i),
x + 20 = √3 × √3x
⇒ 3x – x = 20
⇒ 2x = 20

⇒ x =	20	= 10 metre
	2

∴ Height of pole
= (20 + 10) metre
= 30 metre