Digital electronics miscellaneous
- To add two m-bit numbers, the required number of half adder is—
-
View Hint View Answer Discuss in Forum
To add two m-bit numbers, the required no. of half adder is 2m–1.
Correct Option: A
To add two m-bit numbers, the required no. of half adder is 2m–1.
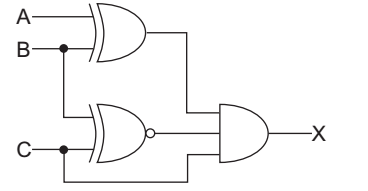
- Consider the following logic circuit. What is the required input condition (A, B, C) to make the output X = 1?
-
View Hint View Answer Discuss in Forum
To get X = 1 output of EX-OR gate and EX - NOR gate must be 1 and in order to make
Y1 = 1 → A should be 0 and B should be 1
Y2 = 1 → C should be 1 and B should be 1. So, to
get X = 1 the condition (0, 1, 1) is correct.
Correct Option: D
To get X = 1 output of EX-OR gate and EX - NOR gate must be 1 and in order to make
Y1 = 1 → A should be 0 and B should be 1
Y2 = 1 → C should be 1 and B should be 1. So, to
get X = 1 the condition (0, 1, 1) is correct.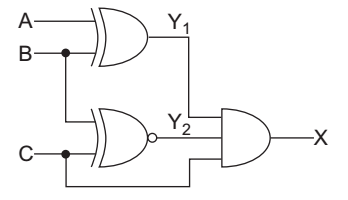
- In Boolean algebra if F = (A + B) ( A + C), then—
-
View Hint View Answer Discuss in Forum
Given, F = (A + B) ( A + C)
or F = AA + AB + BC + AC
or F = AB + BC + AC
To minimize this function, it can be solved easily by using K-map given below:
From K-map, we get F = AB + AC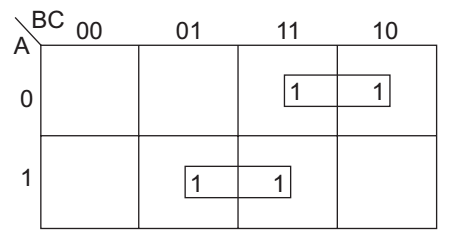
Correct Option: C
Given, F = (A + B) ( A + C)
or F = AA + AB + BC + AC
or F = AB + BC + AC
To minimize this function, it can be solved easily by using K-map given below:
From K-map, we get F = AB + AC
- What is the minimum number of NAND gates required to implement A + AB + AB C?
-
View Hint View Answer Discuss in Forum
Given, F = A + AB + ABC
or F = A (1 + B) + ABC
or F = A + ABC [since 1 + B = 1]
or F = A (1 + BC)
or F = A [since 1 + BC = 1)
Therefore, minimum number of NAND gate required to implement F = A is zero.Correct Option: A
Given, F = A + AB + ABC
or F = A (1 + B) + ABC
or F = A + ABC [since 1 + B = 1]
or F = A (1 + BC)
or F = A [since 1 + BC = 1)
Therefore, minimum number of NAND gate required to implement F = A is zero.
- When signed numbers are used in binary arithmetic, then which one of the following notations would have unique representation for zero?
-
View Hint View Answer Discuss in Forum
When signed numbers are used in binary arithmetic, then 2’S complement notation would have unique representation for zero.
Correct Option: C
When signed numbers are used in binary arithmetic, then 2’S complement notation would have unique representation for zero.

