101. The product of two fractions is 14/15 and their quotient is 35/24 The greater of the fractions is

1. 1. 7

      4

   
   
   

   2. 7

      6

   
   
   

   3. 7

      3

   
   
   

   4. 4

      5

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let us assume the two fractions are p and q, where p > q
   According to given question,
   

   ∴  pq =	14	and	p	=	35
   	15		q		24

   
   Solve this equation to get the answer.

   Correct Option: B

   Let us assume the two fractions are p and q, where p > q
   According to given question,
   

   ∴  pq =	14	and	p	=	35
   	15		q		24

   
   multiply both the given equation and we will get,
   

   ∴  pq ×	p	=	14	×	35
   	q		15		24

   
   

   ⇒  p2 =	49
   	36

   
   

   ⇒  p =	7
   	6

---

102. In an examination, a student was asked to find 3/14 of a certain number, By mistake, he found 3/4 of it. His answer was 150 more than the correct answer. The given number is :

1. 1. 500

   
   
   

   2. 280

   
   
   

   3. 240

   
   
   

   4. 180

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let us assume the number is p.
   According to given question,
   

   3	p −	3	p = 150
   4		14

   
   

   ⇒	21p − 6p	= 150
   	28

   
   Solve this equation further to get the answer.
   

   Correct Option: B

   Let us assume the number is p.
   According to given question,
   

   3	p −	3	p = 150
   4		14

   
   

   ⇒	21p − 6p	= 150
   	28

   
   ⇒  15p = 28 × 150
   

   ⇒  p =	28 × 150	= 280
   	15

---

---

103. A candidate in an examination was asked to find 5/14 of a certain number. By mistake he found 5/14 of it. Thus, his answer was 25 more than the correct answer. The number was :

1. 1. 28

   
   
   

   2. 56

   
   
   

   3. 84

   
   
   

   4. 140

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Let us assume the required number be n.
   As per given question,
   

   ⇒  n ×	5	− n ×	5	= 25
   	4		14

   
   Solve this equation further to get the answer.

   Correct Option: A

   Let us assume the required number be n.
   As per given question,
   

   ⇒  n ×	5	− n ×	5	= 25
   	4		14

   
   

   ⇒ 5n		1	−	1		= 25
   		4		14

   
   

   ⇒ 5n		7 − 2		= 25   ⇒   5n ×	5	= 25
   		28			28

   
   

   ⇒  n =	25 × 28	= 28
   	5 × 5

---

104. The least number that should be added to 2055, so that the sum is exactly divisible by 27 is

1. 1. 28

   
   
   

   2. 24

   
   
   

   3. 27

   
   
   

   4. 31

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   
   

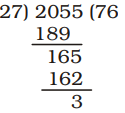
   Correct Option: B

   
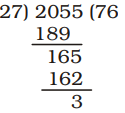
   ∴  Required number = 27 – 3 = 24

---

---

105. If a and b are two odd positive integers, by which of the following integers is (a⁴ – b⁴) always divisible ?

1. 1. 3

   
   
   

   2. 6

   
   
   

   3. 8

   
   
   

   4. 12

   
   
   

---

1. View Hint View Answer Discuss in Forum

   We know that , a⁴ – b⁴ = (a²)² – (b²)² = (a² + b²) (a² − b²) = (a² + b²) (a + b) (a – b)

   Correct Option: C

   We know that , a⁴ – b⁴ = (a²)² – (b²)² = (a² + b²) (a² − b²) = (a² + b²) (a + b) (a – b)
   Let a = 3, b = 1
   ∴  Required number = ( 3 + 1 ) ( 3 – 1 ) = 4 x 2 = 8

---