Mensuration
- The length of the diagonal of a square is ‘a’ cm. Which of the following represents the area of the square (in sq. cm.) ?
-
View Hint View Answer Discuss in Forum
Using Rule 10,
Side of square = Diagonal = a √2 √2
∴ Area = (Side)²= 
a 
² aq.cm. = a² sq.cm. √2 2 Correct Option: C
Using Rule 10,
Side of square = Diagonal = a √2 √2
∴ Area = (Side)²= 
a 
² aq.cm. = a² sq.cm. √2 2
- The sides of a triangle are 3 cm, 4 cm and 5 cm. The area (in cm²) of the triangle formed by joining the mid points of this triangle is :
-
View Hint View Answer Discuss in Forum
Using Rule 1,
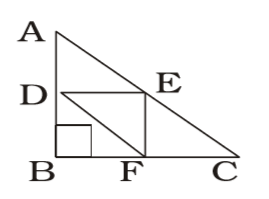
3² + 4² = 5²
∆ ABC is a right angled triangle.∴ area ABC = 1 × AB × BC 2 = 1 × 3 × 4 = 6cm² 2
∴ Required Area of ∆ DEF∴ 1 × 6 = 3 sq.cm. 4 2 Correct Option: C
Using Rule 1,

3² + 4² = 5²
∆ ABC is a right angled triangle.∴ area ABC = 1 × AB × BC 2 = 1 × 3 × 4 = 6cm² 2
∴ Required Area of ∆ DEF∴ 1 × 6 = 3 sq.cm. 4 2
- What is the area of a triangle having perimeter 32cm, one side 11cm and difference of other two sides 5cm?
-
View Hint View Answer Discuss in Forum
Using Rule 2 and 3,
Let the sides of triangle be a, b and c respectively.
∴ 2s = a + b + c = 32
⇒ 11 + b + c = 32
⇒ b + c = 32 – 11 = 21 .....(i)
and b – c = 5 ......(ii)
By adding equations (i) and (ii)
2b = 26 ⇒ b = 13
⇒ c = 13 – 5 = 8
Now, 2s = 32 ⇒ s = 16 a = 11, b = 13, c = 8
∴ Area of triangle
= √s(s - a)(s - b)(s - c)
= √16(16 - 11)(16 - 13)(16 - 8)
= √16 × 5 × 3 × 8
= 8√30 sq. cm.Correct Option: A
Using Rule 2 and 3,
Let the sides of triangle be a, b and c respectively.
∴ 2s = a + b + c = 32
⇒ 11 + b + c = 32
⇒ b + c = 32 – 11 = 21 .....(i)
and b – c = 5 ......(ii)
By adding equations (i) and (ii)
2b = 26 ⇒ b = 13
⇒ c = 13 – 5 = 8
Now, 2s = 32 ⇒ s = 16 a = 11, b = 13, c = 8
∴ Area of triangle
= √s(s - a)(s - b)(s - c)
= √16(16 - 11)(16 - 13)(16 - 8)
= √16 × 5 × 3 × 8
= 8√30 sq. cm.
- The area of circle whose radius is 6 cm is trisected by two concentric circles. The radius of the smallest circle is
-
View Hint View Answer Discuss in Forum
Using Rule 14,
Area of original circle = π × (6)2 = 36π cm²
After trisection, the area of the smallest circle= 1 × 36π = 12π 3
= π × (2√3)²
∴ Required radius = 2√3cmCorrect Option: A
Using Rule 14,
Area of original circle = π × (6)2 = 36π cm²
After trisection, the area of the smallest circle= 1 × 36π = 12π 3
= π × (2√3)²
∴ Required radius = 2√3cm
- If in a ∆ABC, the medians CD and BE intersect each other at 0, then the ratio of the areas of ∆ODE and ∆ABC is
-
View Hint View Answer Discuss in Forum
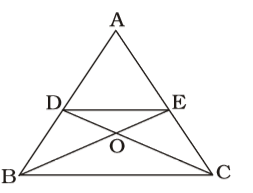
In ∆s ODE and BOC,
∠BOC = ∠DOE
∠DEO = ∠OBC; ∠ODE = ∠OCB
∴ Both triangles are similar,∴ ∆ODE = DE² ∆BOC BC²
DE || BC and DE = 1/2 BC
and area of ∆ ABC
= 3 × Area of ∆OBC∴ ∆ODE = 1 × 1 = 1 ∆ABC 3 4 12
or, 1 : 12Correct Option: C

In ∆s ODE and BOC,
∠BOC = ∠DOE
∠DEO = ∠OBC; ∠ODE = ∠OCB
∴ Both triangles are similar,∴ ∆ODE = DE² ∆BOC BC²
DE || BC and DE = 1/2 BC
and area of ∆ ABC
= 3 × Area of ∆OBC∴ ∆ODE = 1 × 1 = 1 ∆ABC 3 4 12
or, 1 : 12

