Mensuration
- A semicircular sheet of metal of diameter 28 cm is bent into an open conical cup. The capacity of the cup (taking π = 22/7) is
-
View Hint View Answer Discuss in Forum
Let the radius of the base of cup be r cm, 2πr = π × 14
π r = 7 cm
Slant height = 14 cm;
Height = √14² - 7⊃ = √21 × 7
= 7√3 cm∴ Capacity of cup = 1 πr²h 3 = 1 × 22 × 7 × 7 × 7√3 cm 3 7
= 622.36 cubic cm.Correct Option: B
Let the radius of the base of cup be r cm, 2πr = π × 14
π r = 7 cm
Slant height = 14 cm;
Height = √14² - 7⊃ = √21 × 7
= 7√3 cm∴ Capacity of cup = 1 πr²h 3 = 1 × 22 × 7 × 7 × 7√3 cm 3 7
= 622.36 cubic cm.
- In a cylindrical vessel of diameter 24 cm filled up with sufficient quantity of water, a solid spherical ball of radius 6 cm is completely immersed. Then the increase in height of water level is :
-
View Hint View Answer Discuss in Forum
If the height of increased water level be h cm, then
⇒ h = 3 3 ⇒ 12 × 12 × h = 4 × 6 × 6 × 6 3 ⇒ h = 4 × 2 × 6 × 6 2cm 12 × 12 Correct Option: B
If the height of increased water level be h cm, then
⇒ h = 3 3 ⇒ 12 × 12 × h = 4 × 6 × 6 × 6 3 ⇒ h = 4 × 2 × 6 × 6 2cm 12 × 12
- The area of a triangle formed by y = x, x = 6 and y = 0 is :
-
View Hint View Answer Discuss in Forum
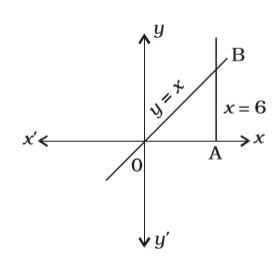
Co-ordinates of point B = (6, 6) as y = x and x = 6
∴ OA = 6 and AB = 6
∴ Area of ∆OAB= 1 × OA × AB 2 = 1 × 6 × 6 = 18 sq. units 2 Correct Option: B

Co-ordinates of point B = (6, 6) as y = x and x = 6
∴ OA = 6 and AB = 6
∴ Area of ∆OAB= 1 × OA × AB 2 = 1 × 6 × 6 = 18 sq. units 2
- The ratio of height and the diameter of a right circular cone is 3 : 2 and its volumeis 1078 cc, then (taking π = 22/7) its height is :
-
View Hint View Answer Discuss in Forum
Let, Height of the cone = 3x cm and diameter = 2x cm.
∴ Radius = x cm.Volume = 1 πr²h 3 ⇒ 1078 = 1 × 22 × x² × 3x 3 7 ⇒ 1078 = 22 x³ 7 ⇒ x³ = 1078 × 7 = 343 22
⇒ x = 3√343 = 7
∴ Height = 3 × 7 = 21 cmCorrect Option: C
Let, Height of the cone = 3x cm and diameter = 2x cm.
∴ Radius = x cm.Volume = 1 πr²h 3 ⇒ 1078 = 1 × 22 × x² × 3x 3 7 ⇒ 1078 = 22 x³ 7 ⇒ x³ = 1078 × 7 = 343 22
⇒ x = 3√343 = 7
∴ Height = 3 × 7 = 21 cm
- The radii of the base of two cylinders A and B are in the ratio 3 : 2 and their height in the ratio n : 1. If the volume of cylinder A is 3 times that of cylinder B, the value of n is
-
View Hint View Answer Discuss in Forum
Let the radius of the base of cylinder A be 3x units and that of cylinder B be 2x units.
Similarly, height of cylinder A = ny units and that of cylinder B be y units.
Since, Volume of cylinder = πr²h
According to the question π(3x)² × ny = 3π (2x)² × y
⇒ 9x²y.n = 12x²y⇒ n = 12 = 4 9 3 Correct Option: A
Let the radius of the base of cylinder A be 3x units and that of cylinder B be 2x units.
Similarly, height of cylinder A = ny units and that of cylinder B be y units.
Since, Volume of cylinder = πr²h
According to the question π(3x)² × ny = 3π (2x)² × y
⇒ 9x²y.n = 12x²y⇒ n = 12 = 4 9 3

