-
If in a ∆ABC, the medians CD and BE intersect each other at 0, then the ratio of the areas of ∆ODE and ∆ABC is
-
- 1 : 6
- 6 : 1
- 1 : 12
- l2 : 1
- 1 : 6
Correct Option: C
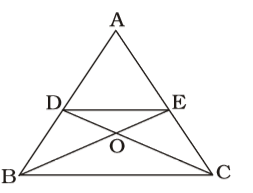
In ∆s ODE and BOC,
∠BOC = ∠DOE
∠DEO = ∠OBC; ∠ODE = ∠OCB
∴ Both triangles are similar,
| ∴ | = | ||
| ∆BOC | BC² |
DE || BC and DE = 1/2 BC
and area of ∆ ABC
= 3 × Area of ∆OBC
| ∴ | = | × | = | ||||
| ∆ABC | 3 | 4 | 12 |
or, 1 : 12

