Syllogism
Syllogism is one of the most important chapter for any aptitude exam. In these type of questions, a premise has generally two statement on the basis of which a deduction has to be made for conclusion. And then after deriving that conclusion we have to select from the given options
We may have a case where from the given premise, no conclusion can be drawn.
Types of Statement
(1) All
(2) Some
(3) No
(4) Some Not
Note:- All and Some are positive and No and Some Not are negative statement.
How To Draw The Figures
Statement
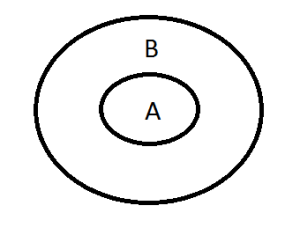
All A are B
Statement
Some A is B
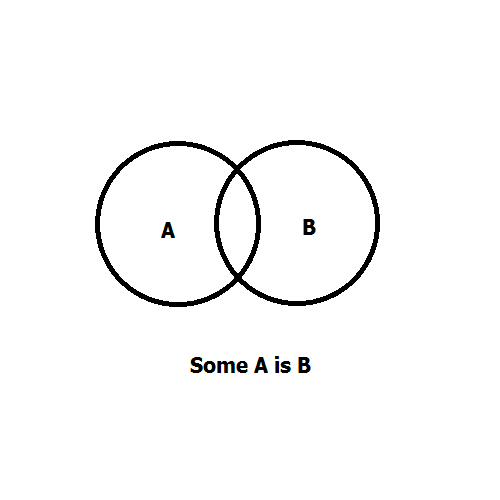
Statement
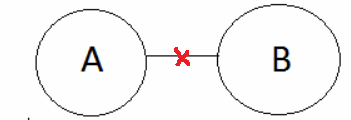
Some A is not B
There are two methods to solve these types of questions:
(i) Venn Diagram
(ii) Rules of deduction
Now we will see how to derive conclusion from the given premise from these two methods. But before that, lets have a look at different components of the premise and for that take two example of premise.
All Rats are Hats …(i)
All Hats are Pats …(ii)
(i) The premises normally start with qualifiers or quantifiers e.g the word All, No, some.The word “All” has its synonyms as – Every, Any, Each, whereas the word “Some” can also be replaced by Many, Few, A little, Most of, Much of, More, etc.
(ii) A premise consists of a subject and a predicate wherein the first term [e.g. “Rats” in statement (i)] is the subject and the second term [e.g. “Hats” in statement (i)] the predicate. Similarly, in statement (ii), ‘Hats” is called the subject and “Pats” is the predicate.
(iii) The word that occurs in both the premises is known as the ‘middle term’ (in this example since “Hats” is in both the premise hence it is called middle term).
(iv) The “conclusion” of the premise middle term should not appear and conclusion should consist of the other two words (“Rats” and “Pats” in the above example) and the.
The premises can be divided into 2 types (Based on type of qualifier): (A) Universal statements [if the qualifier used in the premise is “All”, “Every”, “Any”, “Each”]
(B) Particular statements [if the qualifier used in the premise is “Some”, Many, Few, A little, Most of, Much of, More, etc]
The premises can be divided into 2 types (Based on type of statement):
Positive (affirmative) statements [if premise has no negation]
Negative statements [If premise has a negative term like “not” or “no”]
The combination of the two different categories of classifications leads to four different premises as given in Table below.
The subject or the predicate can be either distributed or not distributed in the given premise. The subject and the predicate are either distributed (indicated as yes) or not distributed (indicated as no) depending on what kind of a statement it is.
Table below shows the distribution pattern of the subject and the predicate.

Please note that:
(i) Subject is distributed only in Universal statements.
(ii) Predicate is distribute in Negative statement.
RULES FOR DEDUCTIONS
1.Every deduction should contain three and only three distinct terms.
2. The middle term must be distributed at least once in the premises.
3. If one premise is negative, then the conclusion must be negative.
4. If one premise is particular, then the conclusion must be particular.
5. If both the premises are negative, no conclusion can be drawn.
6. If both the premises are particular, no conclusion can be drawn.
7. No term can be distributed in the conclusion, if it is not distributed in the premises.
Now lets take few examples to understand this:
Example 1: Find the conclusion of
(i) All Rats are Pats
(ii) All Pats are Cats
Solution: Now look at the minute details of each premise
(i) Here the first statement starts with “All” which is Universal affirmative hence it is a universal affirmative statement, and the subject (Rats) is distributed but the predicate (Pats) is not distributed.
(ii) The second statement is also Universal affirmative, the subject Pats is distributed and the predicate Cats is not distributed.
(iii) Here the middle term is Pats as it occurs in both the premises.
(iv) Middle term is Pats is distributed once in the premises (In this example Premise (ii) hence it satisfies Rule [2] hence we can find a conclusion.
(v) Conclusion will have two terms and these terms are “Rats” and “Cats”
(vi) As “Rats” is distributed in the 1st premises and “Cats” is not distributed,
(vii) In final conclusion “Rats” is distributed but “Cats” is not distributed. Conclusion: All Rats are Cats
Note of Caution: The conclusion can not be All Cats are Rats as in this case we have distributed the
Let Us Study the various possible cases along with Venn Diagram with all possible inferences.
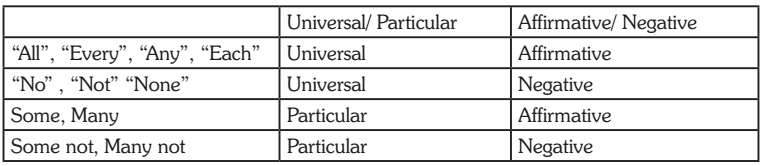
Case 1. All fruits are flowers. All flowers are leafs
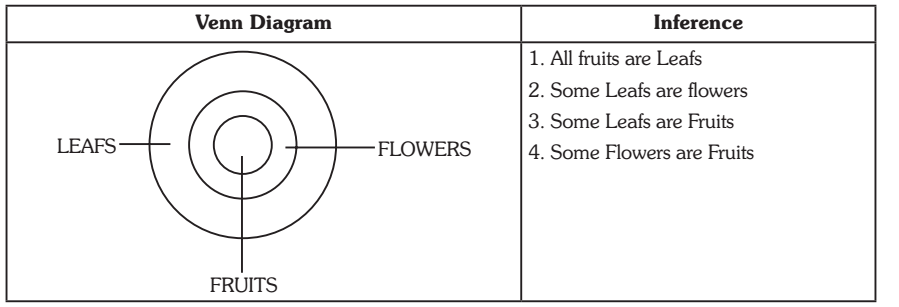
Case 2. ALL P are Q. ALL R are Q.
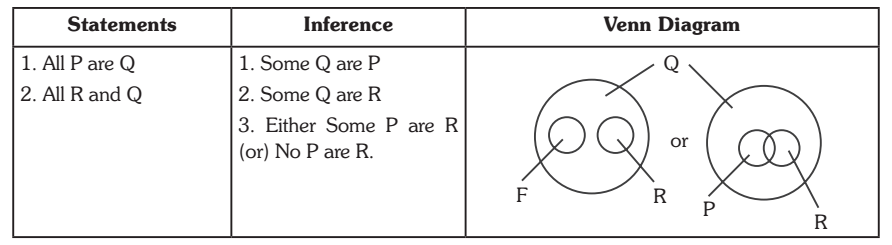
Case 3. All K are M. Some M are S. Statements
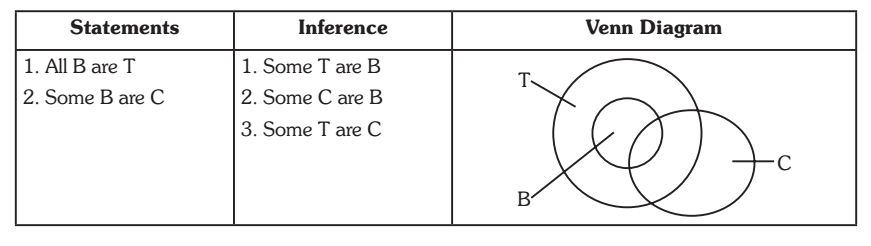
Case 4. All Bs are Ts. Some Bs are Cs. Statements Inference
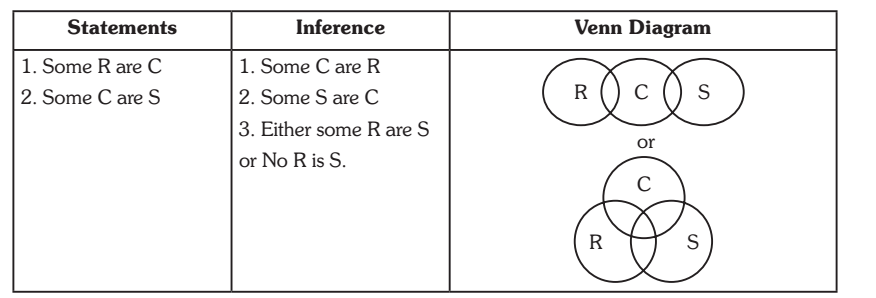
Case 5. Some Rs are Cs. Some Cs are S.
Case 6. All C are D. No D is P.

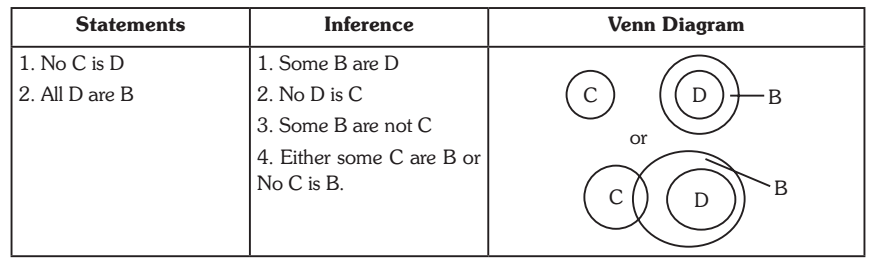
Case 7. No C is D. All D are B
Case 8. No C is D. Some C are L

Direction (Qs. 1-15): In each of the question below are two statements following by two conclusions numbered I and II. You have to take the three given statements to be true even if they seem to be at variance with commonly known facts and then decide which of the given conclusion logically follows from the two statements disregarding commonly known fact.
Give answers:
(a) if conclusion I follows
(b) if conclusion II follows
(c) if either conclusion I or II follows
(d) if neither conclusion I nor II follows
(e) if both conclusion I and II follows
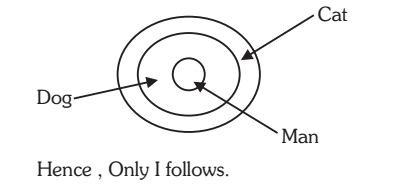
1.Statements: All men are dogs. All dogs are cats.
Conclusions. I. All men are Cats.
II. All cats are men.
Solution:- 1. (a) Since both the premises are universal and affirmative, the conclusion must be universal affirmative. However, conclusion II, being an A-type proposition, distributes the term ‘goats’. Since the term ‘goats’ is distributed in II, without being distributed in any of the premises, so conclusion II cannot follow. Thus, only I follows. Venn Diagram:
2. Statements: All pen are roads. All roads are houses.
Conclusions: I. All Houses are pens,
II. Some houses are pens
Solution:- 2. (b) Since both the premises are universal and affirmative, the conclusion must be universal affirmative and should not contain the middle term. So, it follows that ‘All pens are houses’. II is the converse of this conclusion and so it holds. Since the term ‘houses’. II is the converse of this conclusion and so it holds. Since the term ‘houses’ is distributed in I without being distributed in any of the premises, so I does not follow. Ven Diagram:
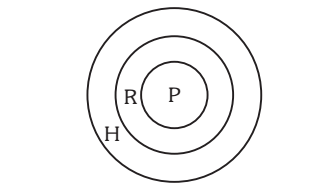
3. Statements: All pens are chalks. All chairs are chalks.
Conclusions: I. Some pens are Chalks.
II. Some chalks are pens.
Solution:- 3. (b) Since the middle term ‘chalks’ is not distributed even once in the premises, no definite conclusion follows. However, II is the converse of the first premise and so it holds.
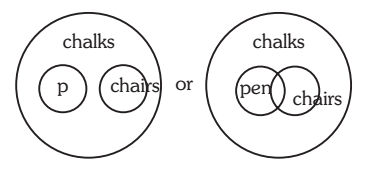
4. Statements: Every Minister is a student. Every student is inexperienced. Conclusions: I. Every Minister is inexperienced.
II. Some inexperienced are students.
Solution:- 4. (e) ‘Every’ is equivalent to ‘All’. Thus, since both the premises are universal and affirmative, the conclusion must be universal affirmative and should not contain the middle term. So, I follows. II is the converse of the second premise and thus it also holds.
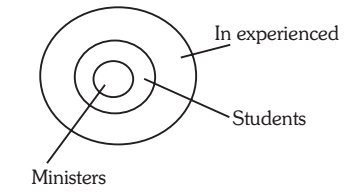
5. Statements: All jungles are tigers. Some tigers are horses.
Conclusions: I. Some horses are jungles.
II. No horse is jungles.
Solution:-5. (c) Since the middle term ‘tigers’ is not distributed even once in the premises, no definite conclusion follows. However, I and II involve only the extreme terms and form a complementary pair. So, either I or II follows.
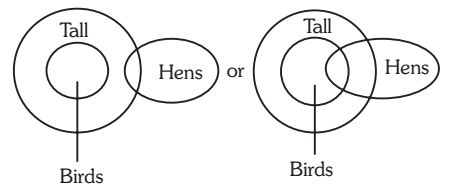
6. Statements: All birds are tall. Some tall are hens.
Conclusions: I. Some birds are hens.
II. Some hens are talls.
Solution:- 6. (b) Since the middle term ‘tall’ is not distributed even once in the premises, no definite conclusion follows. However, II is the converse of the second premise and so it holds.
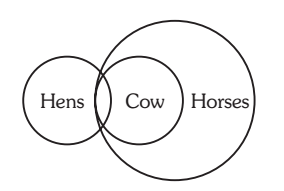
7. Statements: Some hens are cows. All cows are horses.
Conclusions: I. Some horses are hens.
II. Some hens are horses.
Solution:- 7. (e) Since one premise is particular, the conclusion must be particular and should not contain the middle term. So, II follows. I is the converse of II and so it also holds.
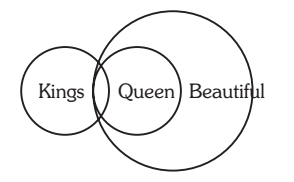
8. Statements: Some KINGs are queens. All queens are beautiful.
Conclusions: I. ALL kings are beautiful.
II. all queens are kings.
Solution:- 8. (d) Since one premise is particular, the conclusion must be particular. So, neither I nor II follows.
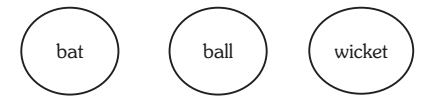
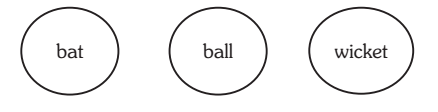
9. Statements: No bat is ball. No ball is wicket.
Conclusions: I. No bat is wicket.
II. All wickets are bats.
Solution:- 9. (d) Since both the premises are negative, no definite conclusion follows.
10. Statements: No women teacher can play. Some women teachers are athletes.
Conclusions: I. Male athletes can play.
II. Some athletes can play.
Solution:- 10. (d) Since one premise is negative, the conclusion must be negative. So, neither conclusion follows.
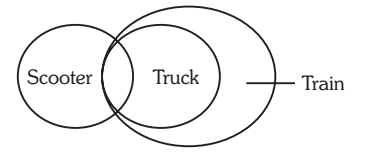
11. Statements: Many scooters are trucks. All trucks are trains.
Conclusions: I. Some Scooters are trains.
II. No truck is a Scooter.
Solution:- 11. (a) Since the first premise is particular, the conclusion must be particular and should not contain the middle term. Thus, only I follows.
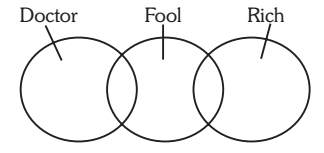
12. Statements: Some doctors are fools. Some fools are rich.
Conclusions: I. Some doctors are rich.
II. Some rich are doctors.
Solution:- 12. (d) Since both the premises are particular, no definite conclusion follows.
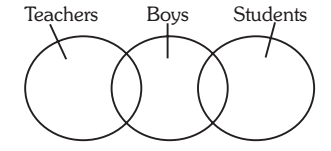
13 Statements: Most teachers are boys. Some boys are students.
Conclusions: I. Some students are boys.
II. Some teachers are Students.
Solution:- 13. (a) Since both the premises are particular, no definite conclusion follows. However, I is the converse of the second Premise and thus it holds.
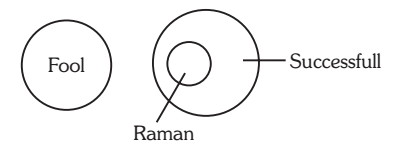
14. Statements: Raman is always successful. No fool is always successful. (IHM)
Conclusions: I. Raman is a fool.
II. Raman is not a fool. Solution:- 14. (b) Since both the premises are universal and one premise is negative, the conclusion must be universal negative and should not contain the middle term. So, only II follows.
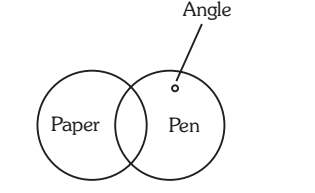
15. Statements: Some papers are pens. Angle is a paper.
Conclusions: I. Angle is not a pen.
II. Angle is a pen.
Solution:- 15. (c) Since the middle term ‘papers’ is not distributed even once in the premises, no definite conclusion follows. However, I and II involve only the extreme terms and form a complementary pair. Thus, either I or II follows.