Grid and Matrices
In this type of questions different numbers are arranged in a matrix with one term missing or numbers are arranged in a wide range of geometrical figures. The numbers in such arrangements follow a certain pattern and you are required to identify that pattern so that you can substitute the question-mark (?) with a suitable number. Now consider the following examples:
In another type of question on operations some equations are solved on the basis of certain system. One ore two solved equations is/are given in the questions statement itself followed by one unsolved equation. You are required to solve that equation after recognizing the rule employed in writing the solved equations.
Now consider the following examples:
Directions: Some equations are solved on the basis of certain system.Find out the correct for the unsolved equation on that basis in each of the following questions:
Ex- 5 × 7 × 9 = 957, 4 × 8 × 6 = 648 and 3 × 7 × 5 =?
Solution:- Delete the signs of multiplication and then write the third digit at the place of hundred’s place, the first digit at ten’s place and the second digit at unit’s place.
5 × 7 × 9 = 957
4 × 8 × 6 = 648
Similarly, 3 × 7 × 5 = 537
Ex- 9 × 6 × 8 × 7 = 7689, 5 × 8 × 6 × 7 = 7865 and 7 × 5 × 6 × 4 =?
Solution:- Delete the signs of multiplication and then write the digits in the following order from left to right: 4th digit, 2nd digit, 3rd digit, 1st digit
9 × 6 × 8 × 7 = 7689
5 × 8 × 6 × 7 = 7865
Similarly, 7 × 5 × 6 × 4 = 4567
Ex- 6 × 7 × 8 = 876, 5 × 6 × 7 = 765 and 4 × 5 × 6 =?
Solution:- Eliminate the signs of multiplication and the write the digits in reverse order.
6 × 7 × 8 = 876
5 × 6 × 7 = 765
Similarly, 4 × 5 × 6 = 654
Directions (1-4): Select the missing number from the given responses:
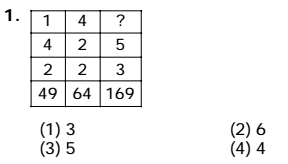
Solution:- (3) The square of the sum of the first three numbers in each column is equal to the lowermost number.
First Column :-
( 1 + 4 + 2 )2 = (7)2 = 49
Second Column :-
( 4 + 2 + 2 )2 = ( 8 )2 = 64
Third Column:- √169 = 13
∴ ? + 5 + 3 = 13
⇒ ? = 13 – 8 = 5
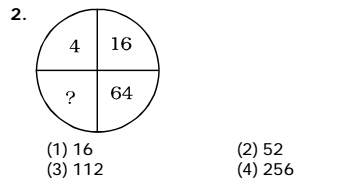
Solution:- (4) 4 × 4 = 16; 16 × 4 = 64; 64 × 4 = 256

Solution:- (1) First Column:-
2 ( 2 + 50 + 10 ) or, 2 × 62 = 124
Second Column:-
2 ( 12 + 300 + 60 ) or, 2 × 372 = 744
Third Column:-
2 ( ? + 550 + 110 ) = 1364
| ? + 660 = | ||
| 2 |
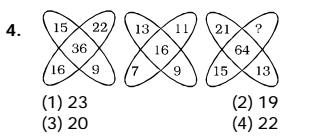
Solution:- (1) First figure:-
15 + 16 = 22 + 9 or, 31 = 31
Second figure:-
13 + 7 = 11 + 9 or, 20 = 20
Third figure:- 21 + 15 =? + 13 or,? = 36 – 13 = 23
SOME MATHEMATICAL PROBLEMS pertaining to the Age, speed and distance, Average etc. are also asked Reasoning Ability Paper. You may find detailed discussion on such topics in the Arithmetic Work Book for SSC Combined Graduate Level (Main) Exam. Never the less, we are citing some such examples:
Ex.1. A train 180 m long is running at a speed of 90 kmph. How long will it take to pass a railway signal?
Answer:
| We know that , Speed = | ||
| Time |
| Here, speed = 90 km/hr = | = 25 m/sec. | |
| 18 |
| ∴ Time = | = 7.2 seconds. | |
| 25 |
Ex.2. The average age of A and B is 54 years, the average age of B and C is 55 years, the average age of C and A is 59 years. What is the age of B in years?
Answer: According to question
Total age of A and B = 54 × 2 = 108 years
Total age of B and C = 110 years
Total age of C and A = 118 years
| ∴ Total age of A, B and C = | = | = 168 years | ||
| 2 | 2 |
Ex.3. A train speeds past a pole in 15 seconds and speeds past a platform of 100 meters in 30 seconds. What is its length in meters?
Answer: Suppose length of train = 1 meters
∴ 1 meters is covered in 15 secs.
∴ In 30 seconds a distance of ( 1 + 100 ) meters is covered
∴ In 15 seconds a distance of ( 1 + 100 )/2 meters is covered
| ∴ 1 = | ⇒ ∴ 1 = 100 | |
| 2 |
Ex.4. If the difference between ages of Babita and Salu is 15 years and ratio of their ages is 3 : 2, then the age of Salu is
Answer: Let the ages of Babita and Salu be x and y years respectively.
∴ According to question,
x – y = 15 years ….(i)
| and | = | ….( ii) | ||
| y | 2 |
| y - y = 15 | ||
| 2 |
Ex.5. One years ago the ratio between Samir’s and Ashok’s age was 4 : 3. One year hence the ratio of their ages will be 5 : 4. What is the sum of their present ages in years?
Answer: Let the present age of Samir and Ashok is x and y years respectively
∴ According to questions,
| = | ||
| ( y - 1 ) | 3 |
or, 3x – 4y = – 1…(i)
Now,
or, 4x + 4 = 5y + 5
or, 4x – 5y = 1…..(ii)
[3x – 4y = – 1] × 4
[4x – 5y = 1] × 3
y = 7 and x = 9
∴ Required sum = 7 + 9= 16 years