Clock and calender
Calendar :-
A calendar is a chart which show the day, week and months of a particular year. A calendar consist of 365 or 366 days divide into 12 months.
Ordinary Year :-
A year in which having 365 days is called an ordinary year. For example- 2011, 2015, 2019 etc.
Leap Year :-
A year in which having 366 days is called leap year. For example- 2000, 2012, 2016 etc.
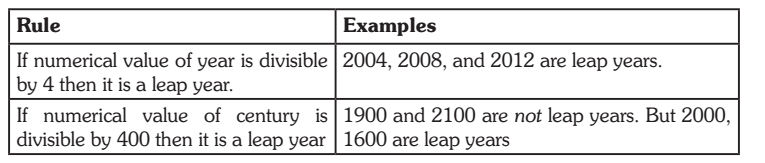
In a century, there are 76 ordinary year and 24 leap years.
Ex- Right now how many century leap year crossed?
Solution:- 400, 800, 1200, 1600, 2000 = 5.
Ex- In 100 years how many leap year are there?
| Solution:- leap years = | = 25 - 1 = 24 | |
| 4 |
How do I find the day of the week for any date?
Method 1. Zeller’s Rule
The following formula is named Zeller’s Rule after a Reverend Zeller. [x] means the greatest integer that is smaller than or equal to x. e.g [2.1] = 2, [3.7] = 3, [499] = 4 and so on
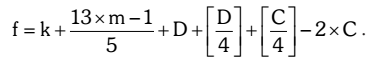
• k is the day of the month. Let’s take 25th June 2013 as an example. For this date, k = 25.
• m is the month number. Months have to be counted specially for Zeller’s Rule: March is 1, April is 2, and so on to February, which is 12. (This makes the formula simpler, because on leap years February 29 is counted as the last day of the year) Because of this rule, January and February are always counted as the 11th and 12th months of the previous year. Means for January 2011 we will use month m = 11 but year we will take as 2010, as new year will begin from March 2011.
In our example,
• m = 4.
• D is the last two digits of the year, D = 13.
• C stands for century: it’s the first two digits of the year. In our case, C = 20.
Now let’s substitute our example numbers into the formula.

F = 25 + 10 + 13 + 3 + 5 – 40 = 16 Now divide this value of f = 16 by 7 remainder is 2.
A remainder of 0 corresponds to Sunday, 1 means Monday, etc
Here remainder 2 means Tuesday.
In this formula we may get value of f as negative. If this is the case then we will add multiple of 7 to make it positive e.g if f = – 17 then f = – 17 + 3 × 7 = 4 so f = – 17 is same as that of 4.
Method 2: The Key Value Method:
In this method we have to memorize few codes but this method is quick and fast in calculation. We’ll take an example of December 20, 1984 as an example.
• Take the last 2 digits of the year. In this case it is 84.
| • Divide it by 4, and find quotient, since = | = 21 | |
| 4 |
• Add the month’s key value, from the following table.

• The month for our example is December, with a key value of 6. Hence 40 + 6 = 46.
• If month is January or February of a leap year, subtract 1. We’re using December, so it is not applicable here.
• Add the century code from the following table.

• Our example year is 1984, and the and get the code 6. Now we add this to our running total: 42 + 6 = 48.
• Add the last two digits of the year. 48 + 82 = 130.
• Divide by 7 and take the remainder. This time, 1 means Sunday, 2 means Monday, and so on. A remainder of 0 means Saturday.
| = 18 ,remainder 4. | ||
| 7 |
So, December 16, 2482 will be on the fourth day of the week-- Wednesday.
SOME MORE INTERESTING POINTS :-
a. A month has either 28 (Non leap year February), 29 (Leap year February), 30 or 31 days.
b. If a month start with Monday, Tuesday, or Wednesday the month will have 4 Saturdays and 4 Sundays i.e total 8 weekends.
c. If a month start with Thursday the month will have 5 Saturdays and 4 Sundays i.e total 9 weekends.
d. If a month start with Friday the month will have 5 Saturdays and 4 Sundays i.e total 9 weekends
e. If month has 28, 29 or 30 days and will have 5 Saturdays and 5 Sundays i.e total 10 weekends if month has 31 days.
f. If a month start with Saturday the month will have 5 Saturdays and 4 Sundays i.e total 9 weekends if month has 28 or 29 days and will have 5 Saturdays and 5 Sundays i.e total 10 weekends if month has 30 or 31 days.
g. If a month start with Sunday the month will have 4 Saturdays and 5 Sundays i.e total 9 weekends.
COUNTING OF ODD DAYS :-
1. 1 ordinary year = 365 days = (52 weeks + 1 day.)
∴ 1 ordinary year has 1 odd day.
2. 1 leap year = 366 days = (52 weeks + 2 days)
∴ 1 leap year has 2 odd days.
3. 100 years = 76 ordinary years + 24 leap years
= (76 × 1 + 24 × 2) odd days = 124 odd days.
= (17 weeks + days) = 5 odd days.
∴ Number of odd days in 100 years = 5.
Number of odd days in 200 years = (5 × 2) ≡ 3 odd days.
Number of odd days in 300 years = (5 × 3) ≡ 1 odd day.
Number of odd days in 400 years = (5 × 4 + 1) ≡ 0 odd day.
Similarly, each one of 800 years, 1200 years, 1600 years, 2000 years etc. has 0 odd days.
Ex. The day before the day before yesterday is three days after Saturday. What day is it today?
(a) Tuesday
(b) Wednesday
(c) Thursday
(d) Friday
Solution:- Three days after Saturday is Tuesday and Tuesday is a day before a day before yesterday So, yesterday is Tuesday.
Hence, today is Friday.
Ex. If 14th October 2005 is Friday then which day is 14th October 2006?
(a) Tuesday
(b) Saturday
(c) Thursday
(d) Friday
Solution:- Since in 1 year we have one odd day while in one leap year we have two odd days.
Number of odd days are 1 (for 2006)
1 days more than Friday means Saturday.
Ex. If 14th October 2005 is Friday then which day is 14th October 2009?
(a) Tuesday
(b) Wednesday
(c) Thursday
(d) Friday
Solution:- Correct Option (b)
Since in 1 year we have one odd day while in one leap year we have two odd days .
Number of odd days are: 1(for 2006) + 1(for 2007) + 2 (For leap year 2008) + 1 (for year 2009) so total number of odd days are 1 + 1 + 2 + 1 = 5 days. 5 days more than Friday means Wednesday.
Ex. If 2nd June 2012 is Saturday then which day is 7th July 2012?
(a) Tuesday
(b) Wednesday
(c) Thursday
(d) Saturday
Solution:- Number of days in June is 30 -2 = 28, and number of days in July is 7, total number of days is 28 + 7 = 35, when we divide 35 by 7 remainder is 0, or number of odd days is 0 hence 7th July must be the same day as that of 2nd June i.e. Saturday in this case.
Ex. If 1st Jan 2001 is Monday then which day was on 1st Jan 2013.
(a) Tuesday
(b) Wednesday
(c) Thursday
(d) Saturday
Solution:- Number of years between 2001 to 2013 is 12 years (2013 - 2001 = 12 years)
Number of leap years between 2001 to 2013 is 3, since a year has 1 odd days and a leap year has 2 odd days , so total number of odd days is 12 + 3 = 15 odd days.
When we divide 15 by 7 remainder is 1 or in total we have 1 odd day so 1st Jan 2013 is Tuesday.
Clock :-
A clock is an instrument having the numbers 1 to 12 or equivalent roman numerals around its face which display time divided into hours, minutes and seconds.

Hour Hand
The smaller or slower hand of a clock is called the hour hand. It takes two revolution in a day.
Minute Hand
The bigger or faster hand of a clock is called the minute hand.
It takes one revolution in every hour.
Second Hand
Second hand bigger or faster then minute hand. It makes one revolution per minute.
Important Points Related to Clock
Angle makes by hour hand and minute hand
Minute Hand:- Minute hand complete one revolution i,e, 360° in 60 minutes.
360° = 60 minutes
180° = 30 minutes
90° = 15 minutes
30° = 5 minutes
6° = 1 minute
∴ 1 minute = 6°
Clearly, minute hand make 6° angle in 1 minute.
Hour hand:- Hour hand complete one revolution i.e, 360° in 12 hours.
12 h = 360°
1 h = 30°
60 min = 30°
| ∴ 1 min = | ||
| 2 |
| Clearly, hour hand make | in 1 minute | |
| 2 |
| Relative Speed between Minute hand and hour hand = 6 - | = 5 | degree per minute. | ||
| 2 | 2 |
Speed of Hour hand and Minute hand :-
Speed of hour hand = 5 min/hour
Speed of minute hand = 60 min/hour
Relative speed = 60 - 5 = 55 min/hour
Note- In every hour, minute hand goes 55 min more than hour hand.
Specific features of hour hand and minute hand :-
When they will make 90° angle.
If two hands are at 90° they are 15 min apart.
Its happens twice in 1 hr.
1 h = 2 times
12 h = 22 times
∴ 1 day = 24 h = 44 times
When they will make 180° angle
If two hands are at 180° they are 30 min apart.
direction opposite to each other.
It happens once in 1 hr.
1 h = 1 times
12 h = 11 times
∴ 1 day = 24 h = 22 times
When they will make a straight line
If angle between minute hand and hour hand is 180°, then they 30 min apart in opposite directly
If angle between minute hand and hour hand is 0°, then no difference between them. ( overlap )
It happens once in 1 hr.
1 h = 1 times
12 h = 11 times
1 day = 24 h = 22 times
Angle between Minute hand and Hour hand :-
Let we have to find angle between minute hand and hour hand at 'H hours and M minutes'.
| Angle between two hands = | M - 30H | |
| 2 |
Ex- Find the angle between minute hand and hour hand at 3 : 20 PM
Solution:- Here, H = 3 and M = 20
According to formula,
| Angle between two hands h hours and m minutes = | M - 30H | |
| 2 |
| = | × 20 - 30 × 3 = 110 - 90 = 20° | |
| 2 |
Ex- Find the angle between minute hand and hour hand at 10 : 10 AM
Solution:- Here, H = 10 and M = 10
According to formula,
| Angle between two hands h hours and m minutes = | M - 30H | |
| 2 |
| = | × 10 - 30 × 10 = 55 - 300 = - 245° | |
| 2 |
Important Formula :-
(1) Two hands at Together
| and ( h + 1 ) O' clock at | h minutes past h. | |
| 11 |
Ex- At what time between 4 PM to 5 PM minute hand and hour hand will be together?
Solution:- Here, h = 4
According to formula,
| Two hands together at = | h minutes | |
| 11 |
| = | × 4 = | = 21 | ||||
| 11 | 11 | 11 |
(2) To hands at Right angle
| ( h + 1 ) O' clock at ( 5h ± 15 ) × | minutes past h. | |
| 11 |
| = ( 5h - 15 ) × | When, h > 6 | |
| 11 |
| = ( 5h + 15 ) × | When, h < 6 | |
| 11 |
Ex- Find the time between 7 and 8 o' clock when two hands are at right angle?
Solution:- Here, h = 7
According to the formula,
| Two hands at right angle = ( 5h - 15 ) × | = ( 5 × 7 - 15 ) × | |||
| 11 | 11 |
| = 20 × | = | = 21 | |||
| 11 | 11 | 11 |
| Hence, they will be at right angle at 7 : 21 | minutes. | |
| 11 |
(3) Two hands at Straight angle
| and (h+1) o' clock at ( 5h ± 30) × | minutes past h. | |
| 11 |
| = ( 5h - 30 ) × | When, h > 6 | |
| 11 |
| = ( 5h + 30 ) × | When, h < 6 | |
| 11 |
Ex- At what time between 3 and 4 o' clock the hand's are in opposite direction?
Solution:- Here, h = 3
According to formula.
| Two hands in opposite direction = ( 5h + 30) × | = ( 5 × 3 + 30 ) × | = 45 × | |||
| 11 | 11 | 11 |
| = | = 49 | ||
| 11 | 11 |
| Hence, they will be at right angle at 3 : 49 | minutes. | |
| 11 |
| and ( h + 1 ) o' clock at ( 5h ± m ) × | minutes past h. | |
| 11 |
Ex- Find the time between 8 and 9 O’clock when the two hands of a clock are 4 minutes apart.
Solution:- Here, h = 8 and m = 4
According to formula,
| = ( 5h ± m ) × | = ( 5 × 8 ± 4 ) × | = ( 40 ± 4) × | |||
| 11 | 11 | 11 |
| = 44 × | and 36 × | = 48 and | |||
| 11 | 11 | 11 |
| the clock losses or gains |  |
- m |  |
 |
 |
minutes. | ||
| 11 | m |
Ex- The minutes hand of a clock overtakes the hour hand at intervals of 70 min of the correct time. how much in a day does the clock gain or loss?
Solution:- Here, m = 60 minutes
According to formula,
| ∴ |  |
- m |  |
 |
 |
|||
| 11 | m |
| = |  |
- 70 |  |
 |
 |
|||
| 11 | 70 |
| = |  |
 |
 |
 |
||||
| 11 | 7 |
| = |  |
 |
 |
 |
||||
| 11 | 7 |
| = | minutes. | |
| 77 |
| = | minutes loss. | |
| 77 |