Signals and systems electrical engineering miscellaneous

Signals and systems electrical engineering miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Signals and Systems

Signals and systems electrical engineering miscellaneous
  1. A sinusoid x(t) of unknown frequency is sampled by an impulse train of period 20 ms. The resulting sample train is next applied to an ideal lowpass filter with a cutoff at 25 Hz. The filter output is seen to be a sinusoid of frequency 20 Hz. This means that x(t) has a frequency of








  1. View Hint View Answer Discuss in Forum

    Sampling rate 50 Hz
    Let x(t) has a frequency of fx Hz,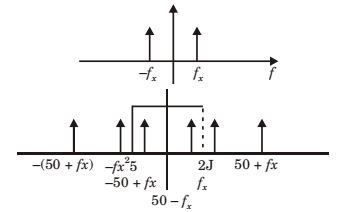

    After sampling with 50 Hz spectrum will be LPF of cut off = 25 Hz
    output = 20 Hz
    ⇒ 50 – fx = 20
    ⇒ fx = 30 Hz Sampling rate 50 Hz
    Let x(t) has a frequency of fx Hz,

    After sampling with 50 Hz spectrum will be LPF of cut off = 25 Hz
    output = 20 Hz
    ⇒ 50 – fx = 20
    ⇒ fx = 30 Hz

    Correct Option: C

    Sampling rate 50 Hz
    Let x(t) has a frequency of fx Hz,

    After sampling with 50 Hz spectrum will be LPF of cut off = 25 Hz
    output = 20 Hz
    ⇒ 50 – fx = 20
    ⇒ fx = 30 Hz

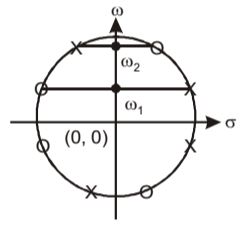
  1. A continuous-time LTI system with system function H(ω) has the following pole-zero plot. For this system, which of the alternatives is TRUE?








  1. View Hint View Answer Discuss in Forum


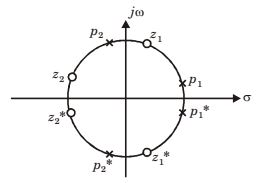
    The transfer function can be written as

    H(s) =
    (s - z1)(s - z1*)(s - z2)(s - z2*)
    (s - P1)(s - P1*)(s - P2)(s - P2*)

    |H(jω)| =
    √ω² + |z1|²√ω² + |z1|²√ω² + |z2|²√ω² + |z2|²
    √s² + |p1|²√ω² + |p1|²√ω² + |p2|²√ω² + |p2|²

    from figure |z1| = |p2|
    |z2| = |p1|
    ⇒ (H(jω)) = K [constant]

    Correct Option: D


    The transfer function can be written as

    H(s) =
    (s - z1)(s - z1*)(s - z2)(s - z2*)
    (s - P1)(s - P1*)(s - P2)(s - P2*)

    |H(jω)| =
    √ω² + |z1|²√ω² + |z1|²√ω² + |z2|²√ω² + |z2|²
    √s² + |p1|²√ω² + |p1|²√ω² + |p2|²√ω² + |p2|²

    from figure |z1| = |p2|
    |z2| = |p1|
    ⇒ (H(jω)) = K [constant]

  1. A signal is represented by
    x(t) =
    1
    		   
    |t| < 1
    0   |t| > 1

    The Fourier transform of the convolved single y(t) = x(2t)*x(t/2) is








  1. View Hint View Answer Discuss in Forum


    Correct Option: A


  1. A function ƒ(t) is shown in the figure.

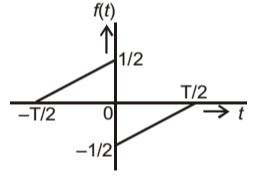
    The Fourier transform F(ω) of ƒ(t) is








  1. View Hint View Answer Discuss in Forum

    Since ƒ(t) is odd and real
    ƒ(t) = – ƒ(– t)
    ∮ F(ω) is imaginary and odd [symmetry property of fourier Transform]

    Correct Option: C

    Since ƒ(t) is odd and real
    ƒ(t) = – ƒ(– t)
    ∮ F(ω) is imaginary and odd [symmetry property of fourier Transform]

  1. A 10 kHz even-symmetric square wave is passed through a bandpass filter with centre frequency at 30 kHz and 3 dB passband of 6 kHz. The filter output is








  1. View Hint View Answer Discuss in Forum

    NA

    Correct Option: C

    NA