-
At a point on a horizontal line through the base of a monument, the angle of elevation of the top of the monument is found to be such that its tangent is 1/5. On walking 138 metres towards the monument the secant of the angle of elevation is found to be
The height of the monument (in metre) is√193 . 12
-
- 35
- 49
- 42
- 56
Correct Option: C
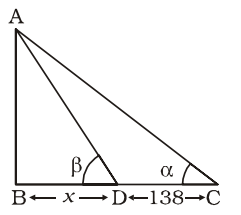
AB = monument = h metre
DC = 138 metre
BD = x metre
| tan α = | 5 |
| sec β = | 12 |
∴ tan β = √sec2 β - 1
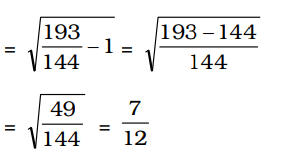
∴ From ∆ABC,
| tan α = | BC |
| ⇒ | = | |||
| 5 | x + 138 |
| ⇒ h = | 5 |
⇒ 5h = x + 138 .............. (i)
From ∆ ABD,
| tan β = | ⇒ | = | ||||
| x | 12 | x |
| ⇒ x = | .........(ii) | 7 |
| ∴ 5h = | + 138 (By (i) & (ii) | 7 |
⇒ 35h – 12h = 138 × 7
⇒ 23 h = 138 × 7
| ⇒ h = | = 42 metre | 23 |

