-
The angle of elevation of sun changes from 30° to 45°, the length of the shadow of a pole decreases by 4 metres, the height of the pole is
( Assume √3 = 1.732)
-
- 1.464 m
- 9.464 m
- 3.648 cm
- 5.464 m
Correct Option: D
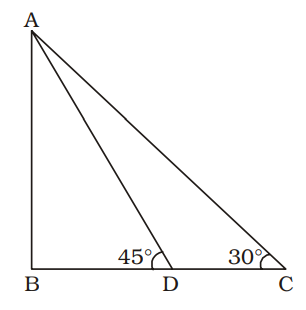
∠ACB = 30°
∠ADB = 45°
CD = 4 metre
AB = pole = h metre
BD = x metre
From ∆ABD
| tan 45° = | BD |
| ⇒ 1 = | ⇒ h = x ......(i) | x |
From ∆ABC,
| tan 30° = | BC |
| ⇒ | = | |||
| √3 | x + 4 |
| ⇒ | = | ⇒ h + 4 | ||
| √3 | h + 4 |
= √3h
⇒ √3h - h = 4
⇒ h( √3 - 1) = 4
| ⇒ h = | = | |||
| √3 - 1 | (√3 - 1)(√3 + 1) |
= 2 (1.732 + 1)
= 2 × 2.732
= 5.464 metre

