ABC is an isosceles triangle where AB = AC which is circumscribed

Home » Aptitude » Plane Geometry » Question

ABC is an isosceles triangle where AB = AC which is circumscribed about a circle. If P is the point where the circle touches the side BC, then which of the following is true?

1. BP = PC
2. BP > PC
3. BP < PC
4. BP = (1/2) PC

Correct Option: A

As per the given in question , we draw a figure of an isosceles triangle ABC which is circumscribed about a circle ,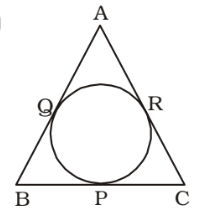

Tangents drawn on a circle from an exterior point are equal.
AQ = AR
∵ AB = AC
∴ BQ = RC
Again, BQ = BP; CP = CR
∴ BP = PC