-
The internal bisectors of the ∠B and ∠C of the ∆ ABC, intersect at O. If ∠A = 100°, then the measure of ∠BOC is :
-
- 140°
- 120°
- 110°
- 130°
- 140°
Correct Option: A
On the basis of given in question , we draw a figure triangle ABC ,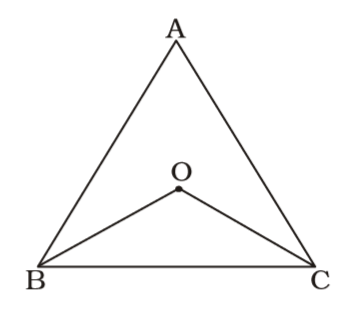
| ∠OBC = | ∠ABC; | |
| 2 |
| ∠OCB = | ∠ACB; | |
| 2 |
From ∆ OBC,
∠OBC + ∠OCB + ∠BOC = 180°
| (∠ABC + ∠ACB) + ∠BOC = 180° | ||
| 2 |
| ⇒ | (180° - ∠BAC) + ∠BOC = 180° | |
| 2 |
| ⇒ | (180° - 100) + ∠BOC = 180° | |
| 2 |
⇒ ∠BOC = 180° – 40° = 140°

