-
In ∆ ABC, the internal bisectors of ∠B and ∠C meet at point O. If ∠A = 80°, then ∠BOC is equal to :
-
- 100°
- 120°
- 130°
- 140°
- 100°
Correct Option: C
We draw a figure triangle whose the internal bisectors of ∠B and ∠C meet at point O , 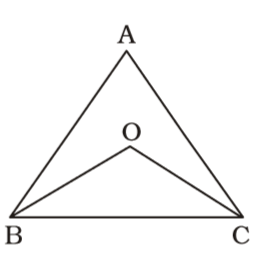
| ∠OBC = | ∠ABC | |
| 2 |
| ∠OCB = | ∠ACB | |
| 2 |
| ∴ ∠OBC + ∠OCB = | (∠ABC + ∠ACB) | |
| 2 |
| ∠OBC + ∠OCB = | (180° - ∠BAC) | |
| 2 |
| ∠OBC + ∠OCB = | (180° - 80°) | |
| 2 |
| ∠OBC + ∠OCB = | = 50° | |
| 2 |
∴ In ∆ OBC,
∠BOC = 180° – (∠OBC + ∠OCB)
Hence , ∠BOC = 180° – 50° = 130°

