-
If cosecθ – sinθ = l and secθ – cosθ = m, then the value of l²m² (l² + m² + 3) is
-
- - 1
- 0
- 1
- 2
Correct Option: C
(l².m²)(m² + 3)
= (cosec θ - sin θ)²
(sec θ - cos θ)²
{(cosec θ - sin θ)² + (sec θ - cos θ)² + 3}
| = | × | sin2θ | cos2θ |
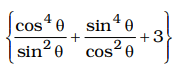
= cos²θ × sin²θ

= cos2 θ + sin6θ + 3cos2θ . sin2θ
= {(cos2θ + sin2θ)
3 – 3 cos2θ . sin2θ(cos2θ + sin2θ)} + 3cos2θ . sin2θ
[∵ a3 + b3 = (a + b)3– 3ab (a + b)]
= 1 – 3 cos2θ . sin2θ + 3 cos2θ .
sin2θ = 1

