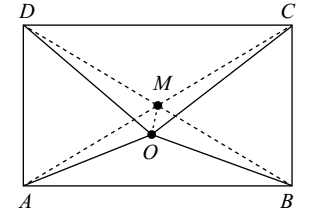
-
A point O in the interior of a rectangular ABCD is joined with each of the vertices A, B, C and D. Then :
-
- OA2 + OC2 = OB2 – OD2
- OA2 + OC2 = OB2 + OD2
- OA2 = OB2 = OC2 + OD2
- OA2 + OD2 = OB2 + OC2
- None of these
Correct Option: B
As per given figure , we can see that
Since the diagonals of a rectangle are equal and bisect each other. Let AC and BD intersect at M. Therefore M is the mid-point of AC and BD and AM = DM
From ΔAOC, OA2 + OC2 = 2(AM2 + MO2) [Appollonius Theorem.] .......... ( 1 )
also in ΔODB, OB2 + OD2 = 2(MO2 + DM2) = 2(MO2 + AM2) .......... ( 2 )
From equations ( 1 ) and ( 2 ) .
∴ OA2 + OC2 = OB2 + OD2.