-
X, Y are the mid-points of opposite sides AB and DC of a parallelogram ABCD. AY and DX are joined intersecting in P; CX and BY are joined intersecting in Q. Then PXQY is a :
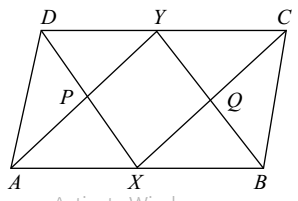
-
- Rectangle
- Rhombus
- Parallelogram
- Square
- None of these
Correct Option: C
From above given figure ,
Proceeding as in Q. No. 4, we can prove that AXCY is a parallelogram .
Similarly, BXDY is a parallelogram.
Now, AXCY is a parallelogram .
⇒ AY || CX
[∴ Opposite sides of a parallelogram are parallel]
⇒ PY || QX …(1)
Also, BXDY is a parallelogram
⇒ DX || BY [∴ Opposite sides of a parallelogram are parallel]
⇒ PX || QY …(2)
Thus, in a quadrilateral PXQY,
From (i) and (ii) ,
we have , PY || QX and PX || QY
⇒ PXQY is a parallelogram.

