-
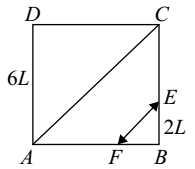
ABCD is a square, F is mid point of AB and E is a point on BC such that BE is one-third of BC. If area of ∆FBE = 108 m2, then the length of AC is:
-
- 63 m
- 36√2 m
- 63√2 m
- 72√2 m
- None of these
Correct Option: B
ABCD is a square . Let, the side of the square be 6L.
Given:- area of ∆FBE = 108 m2
In ∆FBE ,
| Then , Area of triangle = | 1 | × base × height |
| 2 |
| Area of triangle = | 1 | × 3L × 2L = 108 ⇒ 3L2 = 36 ⇒ L = 6 m |
| 2 |
∴ Side of the square = 6 x 6 = 36 m
⇒ AC2 = AD2 + DC2 = (36)2 + (36)2 = 2 × (36)2
⇒ AC = 36√2.