-
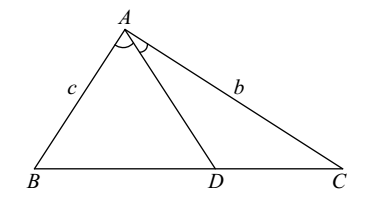
In a Δ ABC, AD intersects ∠ A and BC. If BC = a, AC = b and AB = c, Then :
-
-
CD = b+c ab -
CD = ab b+c -
CD = bc+ab ac -
CD = ac cb+ab - None of these
-
Correct Option: B
From given figure , we have
Since AD bisects ∠BAC
We know that ,
| c | = | BD | (Internal bisector prop.) |
| b | CD |
Adding 1 to both the sides
| c | + 1= | BD | + 1 |
| b | CD |
| c+b | = | BD+CD |
| b | CD |
| c+b | = | a | ⇒CD = | ab |
| b | CD | b+c |
| Similarly it can be proved that BD = | ac | |
| b+c |
Also , BD + CD = BC
| ∴ BD + | ab | = | a |
| b+c |
| ⇒ BD = a - | ab | ⇒ | ab + ac - ab | = | ac |
| b+c | b+c | b+c |