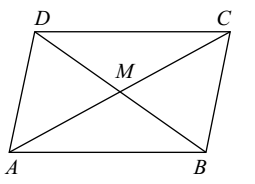
-
If ABCD is a parallelogram and AC and BD be its diagonals, then:
-
- AB2 + BC2+ CD2+ DA2 = AC2 – BD2
- AB2 + BC2+ CD2 + DA2 = AC2 + BD2
- 4AD2 = 2AC2 + 2BD2
- 4AB2 = 2AC2 – 2BC2
- None of these
Correct Option: B
In ||gm ABCD , we have
Since diagonals of parallelogram(||gm ) bisect each other,
∴ M will be the mid-point of each of the diagonal AC and BD
∴ In ΔABC AB2 + BC2 = 2(AM2 + MB2) ......... ( 1 ) [Appolonius Theorem]
In ΔADC AD2 + CD2 = 2(AM2 + DM2) ......... ( 2 )
= 2(AM2 + MB2) [∴ DM = BM]
Adding equations ( 1 ) and ( 2 )
AB2 + BC2 + CD2 + DA2 = 2(AM2 + MB2 + 2(AM2 + MB2 = 4AM2 + 4MB2
= (2AM)2 + (2MB)2= AC2+ BD2. { ∴ AM = MC , MB = MD }