Alligation or Mixture
- A piece of an alloy of two metals (A and B) weighs 15 gms and costs Rs. 150. If the weights of the two metals be interchanged, the new alloy would be worth Rs. 120. If the price of metal A is Rs. 6 per gm, find the weight of the other metal in the original piece of alloy.
-
View Hint View Answer Discuss in Forum
If the two alloys are mixed, the mixture would contain 15 gms of each metal and it would cost Rs. (150 + 120) = Rs. 270.
Cost of (15 gms of metal A + 15 gms of metal B) = Rs. 270
Cost of (1 gm of metal A + 1 gm of metal B) = Rs. (270 / 15) = Rs. 18
Cost of 1 gm of metal B = Rs. (18 – 6) = Rs. 12
Correct Option: C
If the two alloys are mixed, the mixture would contain 15 gms of each metal and it would cost Rs. (150 + 120) = Rs. 270.
Cost of (15 gms of metal A + 15 gms of metal B) = Rs. 270
Cost of (1 gm of metal A + 1 gm of metal B) = Rs. (270 / 15) = Rs. 18
Cost of 1 gm of metal B = Rs. (18 – 6) = Rs. 12
Average cost of original piece of alloy = (150 / 15) = Rs. 10 per gm.
Quantity of metal / A Quantity of metal B = (2 / 4) = (1 / 2)
Quantity of metal B = 2 (1 + 2) × 15 = 10 gms.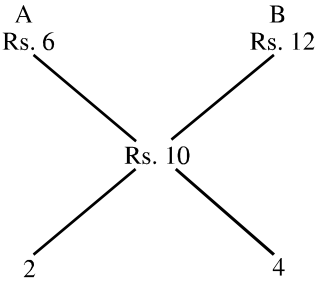
- A vessel contains mixture of liquids A and B in the ratio 3: 2. When 20 litres of the mixture is taken out and replaced by 20 litres of liquid B, the ratio changes to 1: 4. How many litres of liquid A was there initially present in the vessel?
-
View Hint View Answer Discuss in Forum
% of liquid B initially present in the vessel = 2 / (3 + 2) × 100 = 40%
% of liquid B finally present in the vessel = 4 / (1 + 4) × 100 = 80%
The second solution is liquid B which is being mixed and it has 100% liquid B.
80% of liquid B present in the resultant mixture may be taken as average percentage. So, using rule of alligation on liquid B per cent,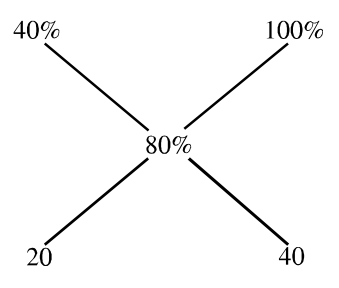
Correct Option: B
21.% of liquid B initially present in the vessel = 2 / (3 + 2) × 100 = 40%
% of liquid B finally present in the vessel = 4 / (1 + 4) × 100 = 80%
The second solution is liquid B which is being mixed and it has 100% liquid B.
80% of liquid B present in the resultant mixture may be taken as average percentage. So, using rule of alligation on liquid B per cent, we can write,
or 1 : 2
The ratio of liquid left in the vessel to liquid B being mixed = 1: 2
Since the quantity of liquid B being mixed is 20 liters, the quantity of liquid left in the vessel is 10 liters.
Therefore, the total quantity of liquid initially present in the vessel = 10 + 20 = 30 liters
Quantity of liquid A = 3 / (2 + 3) × 30 = 18 liters.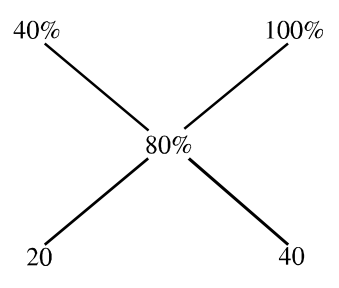
- From a cask of wine containing 25 litres, 5 litres are withdrawn and the cask is refilled with water. The process is repeated a second and then a third time. Find the quantity of wine left in the cask and also the ratio of wine to water in the resulting mixture.
-
View Hint View Answer Discuss in Forum
Here, quantity of wine left after third operation
= [1 - (5 / 25)]3 x 25 = (4 / 5)3 x 25Correct Option: D
Here, quantity of wine left after third operation
= [1 - (5 / 25)]3 x 25 = (4 / 5)3 x 25 = (64 / 125) x 25 = (64 / 5) = 12 4/5 liters.
Final ratio of wine to water = (64 / 125) / (1- 64 /125)
= (64 / 125) /(61 / 125)
Wine : Water = (64 / 61)
- A person covers a distance of 100 kms in 10 hours, partly by walking at 7 km/hr and rest by running at 12 km/hr. Find the distance covered in each part.
-
View Hint View Answer Discuss in Forum
Average speed = (100 / 10) = 10 km/hr.
Ratio of time taken at 7 km/hr to 12 km/hr = 2 : 3
Correct Option: B
Average speed = (100 / 10) = 10 km/hr.
Ratio of time taken at 7 km/hr to 12 km/hr = 2 : 3
Time taken at 7 km/hr = 2 (2 + 3) × 10 = 4 hrs.
Distance covered at 7 km/hr = 7 × 4 = 28 km.
Distance covered at 12 km/hr = 100 – 28 = 72 km.
- Two vessels A and B contain milk and water in the ratio 7 : 5 and 17 : 7 respectively. In what ratio mixtures from two vessels should be mixed to get a new mixture containing milk and water in the ratio 5 : 3?
-
View Hint View Answer Discuss in Forum
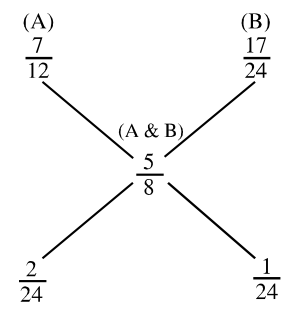
First of all we write the fraction of milk present in three mixtures. In A : 7 /12
In B : 17 /24
In combination of A and B : 5 /8
We now apply allegation rule on these fractions.

Correct Option: B
First of all we write the fraction of milk present in three mixtures. In A : 7 /12
In B : 17 /24
In combination of A and B : 5 /8
We now apply allegation rule on these fractions from figure.
So, Ratio of A: B = 2 : 1
2nd Method
Let us assume P mixture taken from first vessel and Q mixture taken from second vessel to form a new mixture.
Part of Milk in P mixture from first vessel = 7P/12
Part of Milk in Q mixture from Second vessel = 17Q/24
Part of Water in P mixture from first vessel = 5P/12
Part of Milk in Q mixture from Second vessel = 7Q/24
According to question,
After mixing the P and Q, we will get mixture.
Milk in New Mixture / Water in New Mixture = 5/3
{(7P/12) + (17Q/24 ) } /{ (5P/12) + (7Q/24) } = 5/3
{(14P + 17Q)/24 } /{ (10P + (7Q)/24 } = 5/3
{(14P + 17Q) } /{ (10P + (7Q)} = 5/3
(14P + 17Q) x 3 = 5 x (10P + (7Q)
42P + 51Q = 50P + 35Q
51Q - 35Q = 50P - 42P
8P = 16Q
P = 2Q
P/Q = 2
P : Q = 2 : 1