-
Two vessels A and B contain milk and water in the ratio 7 : 5 and 17 : 7 respectively. In what ratio mixtures from two vessels should be mixed to get a new mixture containing milk and water in the ratio 5 : 3?
-
- 1 : 2
- 2 : 1
- 2 : 3
- 3 : 2
Correct Option: B
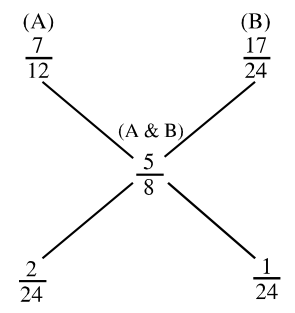
First of all we write the fraction of milk present in three mixtures. In A : 7 /12
In B : 17 /24
In combination of A and B : 5 /8
We now apply allegation rule on these fractions from figure.
So, Ratio of A: B = 2 : 1
2nd Method
Let us assume P mixture taken from first vessel and Q mixture taken from second vessel to form a new mixture.
Part of Milk in P mixture from first vessel = 7P/12
Part of Milk in Q mixture from Second vessel = 17Q/24
Part of Water in P mixture from first vessel = 5P/12
Part of Milk in Q mixture from Second vessel = 7Q/24
According to question,
After mixing the P and Q, we will get mixture.
Milk in New Mixture / Water in New Mixture = 5/3
{(7P/12) + (17Q/24 ) } /{ (5P/12) + (7Q/24) } = 5/3
{(14P + 17Q)/24 } /{ (10P + (7Q)/24 } = 5/3
{(14P + 17Q) } /{ (10P + (7Q)} = 5/3
(14P + 17Q) x 3 = 5 x (10P + (7Q)
42P + 51Q = 50P + 35Q
51Q - 35Q = 50P - 42P
8P = 16Q
P = 2Q
P/Q = 2
P : Q = 2 : 1