Alligation or Mixture
- A cask full of wine from which 8 litres are drawn and is then filled with water. This operation is performed three more times. The ratio of quantity of wine left in the cask to that of the water is 16: 81. How much wine did the cask hold originally?
-
View Hint View Answer Discuss in Forum
Let A liters wine cask hold originally, then
A[1 - (8 / A )]4 / A = 16 / 81Correct Option: C
Let A liters wine cask hold originally, then
A[1 - (8 / A)]4 / A = 16 / 81
⇒ (1 - (8 / A))4 = (2 / 3 )4
⇒ (1 - (8 / A)) = (2 / 3)
⇒ (8 / A) = (1 - (2 /3))
⇒ (8 / A) = (1 / 3)
∴ A = 24 liters
- Some amount out of Rs. 7000 was lent at 6 % p.a. and the remaining at 4 % p. a. If the total simple interest from both the fractions in 5 years was Rs. 1600, the sum lent at 6 % p. a. was —
-
View Hint View Answer Discuss in Forum
According to question ,
Average annual rate = 
1600 × 1000 
% 7000 5 Average annual rate = 
32 
% 7 ∴ (Amount at 6%) : (Amount at 4%) = 4 : 10 = 2 : 5 7 7
Correct Option: A
According to question ,
Average annual rate = 
1600 × 1000 
% 7000 5 Average annual rate = 
32 
% 7 ∴ (Amount at 6%) : (Amount at 4%) = 4 : 10 = 2 : 5 7 7 ∴ Sum lent at 6% = Rs. 
700 × 2 
7
Hence, Sum lent at 6% = Rs. 2000.
- A sum of Rs. 41 was divided among 50 boys and girls. Each boy gets 90 paise and a girl 65 paise. The number of boys is —
-
View Hint View Answer Discuss in Forum
As per the given question , we can say that
Average money received by each = Rs. 41 50
Average money received by each = 82 paise
Correct Option: B
As per the given question , we can say that
Average money received by each = Rs. 41 50
Average money received by each = 82 paise
Ratio of boys and girls = 17 : 8
Total ratios of boys and girls = 17 + 8 = 25∴ Number of boys = 
50 × 17 
25
Therefore ,Number of boys = 34.
- Rs. 675 was divided among 75 boys and girls. Each boy gets Rs. 20 whereas a girl gets Rs. 5. Find the number of boys and girls.
-
View Hint View Answer Discuss in Forum
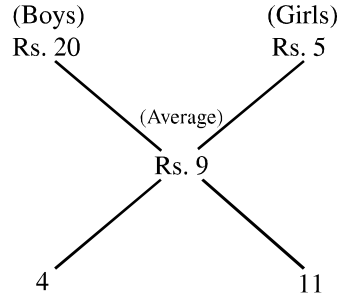
Average money per head (boy or girl) = Rs. (675 / 75) = Rs. 9
Correct Option: A
Average money per head (boy or girl) = Rs. (675 / 75) = Rs. 9
Number of boys = 4 / (4 + 11) × 75 = 20
Number of girls = 11 / (4 + 11) × 75 = 55.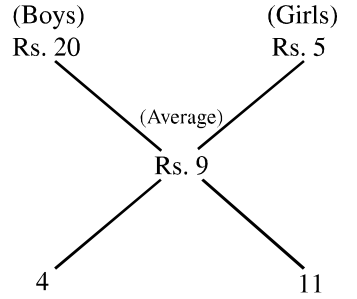
- Sugar at Rs. 15 per kg is mixed with sugar at Rs. 20 per kg in the ratio 2 : 3. Find the price per kg of the mixture—
-
View Hint View Answer Discuss in Forum
Given :- Ratio = 2 : 3 , C1 = 15 kg , C2 = 20 kg and Mean cost Price = Z
Using the alligation rule ,C2 – Z = 2 Z – C1 3 20 – Z = 2 Z – 15 3
Correct Option: A
Given :- Ratio = 2 : 3 , C1 = 15 kg , C2 = 20 kg and Mean cost Price = Z
Using the alligation rule ,C2 – Z = 2 Z – C1 3
∴ Z = Rs. 18 per kg.20 – Z = 2 Z – 15 3

