Alligation or Mixture
- Find the quantity of rice @ Rs. 10 per kg. which should be mixed with 25 kgs of rice @ Rs. 8 per kg, so that on selling the mixture @ Rs. 15 per kg there is 80% profit.
-
View Hint View Answer Discuss in Forum
Cost price of the mixture = 15 × (100 / 180) = Rs. 25/3 per kg
(Quantity of rice @ Rs. 8 per kg) / (Quantity of rice @ Rs.10 per kg) = (5 / 3) / (1/3) = 1/5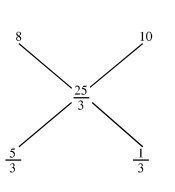
Correct Option: D
Cost price of the mixture = 15 × (100 / 180) = Rs. 25/3 per kg
(Quantity of rice @ Rs. 8 per kg) / (Quantity of rice @ Rs.10 per kg) = (5 / 3) / (1/3) = 1/5
Quantity of rice @ Rs. 10 per kg = 25 × (1/ 5) = 5 kgs.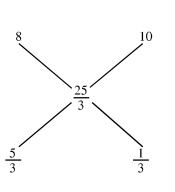
- In what proportion must tea at Rs. 62 per kg be mixed with tea at Rs. 72 per kg in order to obtain the mixture worth Rs. 65 per kg?
-
View Hint View Answer Discuss in Forum
Using Alligation rule,
(Quantity of cheaper tea) / (Quantity of dearer tea) = (d - m) / (m - c)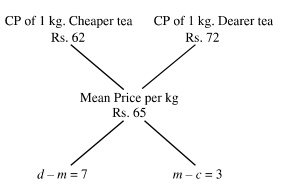
Correct Option: B
Using Alligation rule,
(Quantity of cheaper tea) / (Quantity of dearer tea) = (d - m) / (m - c) = 7/3
Therefore, they must be mixed in the ratio of 7 : 3.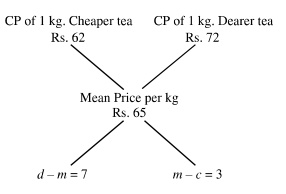
- Two solution of 90% and 97% purity and mixed resulting in 21 liters of mixture of 94% purity. How much is the quantity of the first solution in the resulting mixture?
-
View Hint View Answer Discuss in Forum
Method 1 to solve the equation.
Let us assume the number of liters of the 90% purity solution = A
and the number of liters of the 97% purity solution = B.
According to question,
Since there are 21 liters of the solution,
A + B = 21 ...................... (1)
Since after mixing the two solutions the new mixture has 94% purity,
Concentrate of A + Concentrate of B = Concentrate of (A + B)
A x 90% + B x 94% = (A + B) x 97% .....................(2)
Solve the equation to get the answer.
Method 2 to solve the equation.
Hit and trail method.
94% is closer to 97% but barely meaning the mixtures will not be equal parts but will be slightly more of the higher purity. Quickly eliminate A and B. Out of the others 9 is the easy choice. If the other choices were closer to half this wouldn't work.Correct Option: C
Method 1 to solve the equation.
Let us assume the number of liters of the 90% purity solution = A
and the number of liters of the 97% purity solution = B.
According to question,
Since there are 21 liters of the solution,
A + B = 21 ...................... (1)
Since after mixing the two solutions the new mixture has 94% purity,
Concentrate of A + Concentrate of B = Concentrate of (A + B)
A x 90% + B x 94% = (A+ B) x 97%
⇒ A x 90/100 + B x 97/100 = (A + B) x 94/100
⇒ 90A + 97B = (A + B) x 94
⇒ 90A + 97B = 94A + 94B
⇒ 94A + 94B - 90A- 97B = 0
⇒ 4A - 3B = 0 ........................(2)
Multiply the 3 with Equation (1) and add with Equation (2),
3A + 3B + 4A - 3B = 63 + 0
⇒ 7A = 63
⇒ A = 63/7 = 9
Put the value of A in Equation (1) , we will get
9 + B = 21
B = 21 - 9
B = 12
The first solution would be A = 9 liters.
Method 2 to solve the equation.
Hit and trail method.
94% is closer to 97% but barely meaning the mixtures will not be equal parts but will be slightly more of the higher purity. Quickly eliminate A and B. Out of the others 9 is the easy choice. If the other choices were closer to half this wouldn't work.
- In what ratio should milk and water be mixed so that after selling the mixture at the cost price a profit of 50/3 % is made ?
-
View Hint View Answer Discuss in Forum
Method 1 to solve the equation.
Let us assume Cost Price (C.P) of 1 liter milk be Y rupees.
According to question,
Selling Price (S.P) of 1 liter of mixture Y rupees. (Selling price should be same as Cost price)
Profit = 50/3 %
Let us assume Cost price of 1 Liter of Mixture of Water and Milk = C
Cost price of 1 Liter of Mixture of Water and Milk = Selling price of Mixture - Profit
Solve the equation and get the answer.
Method 2 to solve the question.
Let the original amount of milk be 1 liter and the cost price is 1 rupees per liter.
Cost price of milk CP1 = 1.
Selling price of Mixture SP1 = 1.
Case 2 : When the milk is mix with x liters of water milk remaining is 1- x.
Let us assume the cost price of milk in mixture is Y and given that the Selling Price is 1.
we should use the Profit formula in algebra,
Solve the equation and get the answer.Correct Option: B
Method 1 to solve the equation.
Let us assume Cost Price (C.P) of 1 liter milk be Y rupees.
According to question,
Selling Price (S.P) of 1 liter of mixture Y rupees. (Selling price should be same as Cost price)
Profit = 50/3 %
Let us assume Cost price of 1 Liter of Mixture of Water and Milk = C
Cost price of 1 Liter of Mixture of Water and Milk = Selling price of Mixture - Profit
C = Y - C x 50/3%
⇒ C = Y - C x 50/3x100
⇒ C = Y - C x 1/3x2
⇒ C = Y - C/6
⇒ Y = C + C/6
⇒ Y = (6C + C)/6
⇒ Y = (6C + C)/6
⇒ Y = 7C/6
⇒ C = 6Y/7
Since in Y rupees we will get 1 liter milk.
Hence in 1 rupees we will get 1/Y liter milk.
Hence in 6Y/7 rupees we will get 1 x 6Y/7 x Y liter milk.
Hence in 6Y/7 rupees we will get 6/7 liter milk.
We need 1 liter mixture of milk and water for sold on the same price, we need to mix the water.
So water quantity in mixture = 1 - 6/7 = 1/7
Ratio of Milk and water in mixture = quantity of Milk in Mixture/quantity of Water in Mixture
Ratio of Milk and water in mixture = 6/7 / 1/7
Ratio of Milk and water in mixture = 6 x 7 / 7
Ratio of Milk and water in mixture = 6 / 1
Ratio of Milk and water in mixture = 6 : 1
Method 2 to solve the question.
Let the original amount of milk be 1 liter and the cost price is 1 rupees per liter.
Cost price of milk = 1 rupees.
Selling price of Mixture = 1 rupees.
When the milk is mix with x liters of water milk remaining is 1- x.
Let us assume the cost price of milk in mixture is Y and given that the Sold Price is 1.
we should use the Profit formula in algebra,
Y + Y x 50/3 % = 1
Y + Y x 50/3 x 100 = 1
Y + Y x /3 x 2 = 1
7Y/6 = 1
Y = 6/7
Y = 6/7 is the cost price of Mixture for 1 liter.
Since water is free so there is not cost of water in mixture. So price of milk is 6/7 rs in mixture.
Since as per question,
In 1 rupees we will get 1 liter of milk.
hence in 6/7 rupees we will get 1 x 6/7 = 6/7 liter of milk.
Now we have to make 1 liter of mixture with water and milk.
quantity of Water + Quantity of Milk = 1 liter
quantity of Water + 6/7 = 1
quantity of Water = 1 - 6/7 = (7 - 6)/7
quantity of Water = 1/7
Ratio of milk and Water = Quantity of Milk / quantity of Water
Ratio of milk and Water = (6/7) / (1/7)
Ratio of milk and Water = (6/7) x (7/1)
Ratio of milk and Water = 6 x 7/ 7 x 1
Ratio of milk and Water = 6 :1
- In a class of 30 students , the average weight of boys is 20 kg and the average weight of the girls is 25 kg . The fraction of boys out of the total students of the class is
-
View Hint View Answer Discuss in Forum
Let us assume the number of boys = B and number of girls = G.
According to question,
B + G = 30
Lets us assume total weight of boys = W1 and total weight of girls = W2
average weight of boys = total weight of boys/number of boys
average weight of girls = total weight of girls/number of girlsCorrect Option: D
Let us assume the number of boys = B and number of girls = G.
According to question,
B + G = 30
Lets us assume total weight of boys = W1 and total weight of girls = W2
average weight of boys = total weight of boys/number of boys
total weight of boys/number of boys = 20
W1/B = 20
W1 = 20B
average weight of girls = total weight of girls/number of girls
25 = W2/G
W2 = 25G
Data is not sufficient to solve the equation.
since we do not know either the average weight of the whole class or the ratio of no. of boys to girls.

