Alligation or Mixture
- A merchant has 50 kg. of sugar part of which he sells at 8 % profit and the rest at 18 % profit. He gains 14 % on the whole. The quantity sold at 18 % profit is —
-
View Hint View Answer Discuss in Forum
Here , C1 = 8% , C2 = 18% and Mean Profit ( M ) = 14%
Ratio of 1st and 2nd part = 4 : 6 = 2 : 3
Using the method of alligation ,
Correct Option: B
Here , C1 = 8% , C2 = 18% and Mean Profit ( M ) = 14%
Ratio of 1st and 2nd part = 4 : 6 = 2 : 3Quantity sold at 18% = 
50 × 3 
= 30 kg 2
Using the method of alligation ,

- In a mixture of 60 liters, the ratio of milk and water is 2 : 1. If the ratio of the milk and water is to be 1 : 2, then the amount of water to be further added is —
-
View Hint View Answer Discuss in Forum
Here , Ratio of milk and water in mixture of 60 litre = 2 : 1
∴ Quantity of milk = 2y = 40 litre
Quantity of water = y = 20 litreCorrect Option: D
Here , Ratio of milk and water in mixture of 60 litre = 2 : 1
∴ Quantity of milk = 2y = 40 litre
Quantity of water = y = 20 litre
If ratio of milk and water is to be 1 : 2, then in 40 litres of milk, water should be 80 litre
∴ Quantity of water to be added = 60 litre.
- 729 ml. of a mixture contains milk and water in the ratio 7 : 2. How much more water is to be added to get a new mixture containing milk and water in ratio 7 : 3 ?
-
View Hint View Answer Discuss in Forum
Given :- Quantity of mixture = 729 ml and Ratio of milk and water = 7 : 2
Quantity of Milk = 
729 × 7 
= 567 ml 9
Quantity of Water = (729 – 567) = 162 ml
According to question ,Now, 567 = 7 162 + y 3
Correct Option: D
Given :- Quantity of mixture = 729 ml and Ratio of milk and water = 7 : 2
Quantity of Milk = 
729 × 7 
= 567 ml 9
Quantity of Water = (729 – 567) = 162 ml
According to question ,Now, 567 = 7 162 + y 3
⇒ 567 x 3 = 7 ( 162 + y ) ⇒ 1701 = 1134 + 7y ⇒ 7y = 567
⇒ y = 81 ml .
- A vessel contains 20 liters of a mixture of milk and water in the ratio 3:2. 10 liters of the mixture are removed and replaced with an equal quantity of pure milk. If the process is repeated once more, find the ratio of milk and water in the final mixture obtained ?
-
View Hint View Answer Discuss in Forum
According to question,
Quantity of Milk/Quantity of Water = 3/2
Let us assume the product ratio = n.
Quantity of Milk = 3n and Quantity of Water = 2n
Quantity of Milk + Quantity of Water = 20 liters
3n + 2n = 20 liters
5n = 20 liters
n = 20/5
n = 4
Quantity of Milk = 3n liters
Put the value of n,
Quantity of Milk = 3 x 4 = 12 liters
Quantity of Water = 2n
Quantity of Water = 2 x 4 = 8 liters
If 10 liters of mixture are removed first time, we will find how much milk and water contain in mixture.
∵ 20 liters of mixture contains 12 liter of milk.
∴ 1 liters of mixture contains 12/20 liter of milk.
∴ 10 liters of mixture contains 10 x 12/20 liter of milk.
∴ 10 liters of mixture contains 6 liter of milk.
∴ 10 liters of mixture contains 4 liter of water.
If 10 liters of mixture are removed, then amount of milk removed = 6 liters and amount of water removed = 4 liters.
Remaining milk = 12 - 6 = 6 liters
Remaining water = 8 - 4 = 4 liters
10 liters of pure milk are added, therefore total milk = (6 + 10) = 16 liters and water = 4 liters.
If the process is repeated one more time and 10 liters of the mixture are removed second time, then
If 10 liters of mixture are removed, Again we will find how much milk and water contain in the mixture.
Solve the equation in same way and get the answer.Correct Option: D
According to question,
Quantity of Milk/Quantity of Water = 3/2
Let us assume the product ratio = n.
Quantity of Milk = 3n and Quantity of Water = 2n liters
Quantity of Milk + Quantity of Water = 20 liters
3n + 2n = 20 liters
5n = 20 liters
n = 20/5
n = 4
Quantity of Milk = 3n liters
Put the value of n,
Quantity of Milk = 3 x 4 = 12 liters
Quantity of Water = 2n
Quantity of Water = 2 x 4 = 8 liters
If 10 liters of mixture are removed first time, we will find how much milk and water contain in mixture.
∵ 20 liters of mixture contains 12 liter of milk.
∴ 1 liters of mixture contains 12/20 liter of milk.
∴ 10 liters of mixture contains 10 x 12/20 liter of milk.
∴ 10 liters of mixture contains 6 liter of milk.
∴ 10 liters of mixture contains 4 liter of water.
If 10 liters of mixture are removed, then amount of milk removed = 6 liters and amount of water removed = 4 liters.
Remaining milk = 12 - 6 = 6 liters
Remaining water = 8 - 4 = 4 liters
10 liters of pure milk are added, therefore total milk = (6 + 10) = 16 liters and water = 4 liters.
If the process is repeated one more time and 10 liters of the mixture are removed second time, then
If 10 liters of mixture are removed, Again we will find how much milk and water contain in the mixture.
∵ 20 liters of mixture contains 16 liter of milk.
∴ 1 liters of mixture contains 16/20 liter of milk.
∴ 10 liters of mixture contains 10 x 16/20 liter of milk.
∴ 10 liters of mixture contains 8 liter of milk.
∴ 10 liters of mixture contains 2 liter of water.
If 10 liters of mixture are removed, then amount of milk removed = 8 liters and amount of water removed = 2 liters.
Remaining milk = (16 - 8) = 8 liters.
Remaining water = (4 - 2) = 2 liters.
Now 10 liters milk is added => total milk = 18 liters and water will be 2 liters.
The required ratio of milk and water in the final mixture obtained
Quantity of milk/Quantity of Water= 18:2 = 9:1
- The cost of type - I rice is Rs. 15 per kg and type - II is Rs. 20 per kg. If both type - I and type - II are mixed in the ratio of 2 : 3, then find the price per kg of the mixed variety.
-
View Hint View Answer Discuss in Forum
Let the price per kg of mixed variety be Rs. P.
then By the rule of alligation,
Now, (20 - P) / (P - 15) = (2 / 3)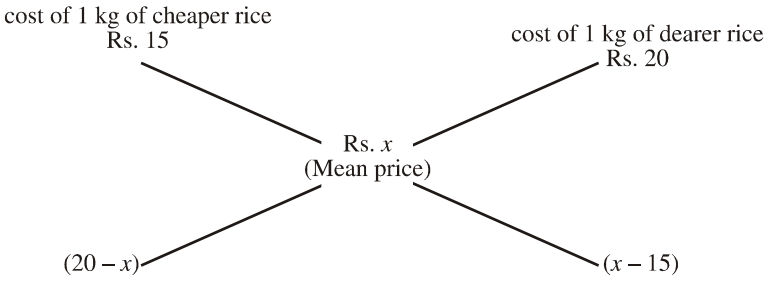
Correct Option: D
Let the price per kg of mixed variety be Rs. P;
then By the rule of alligation,
Now, (20 - P) / (P - 15) = (2 / 3)
⇒ 60 – 3P = 2P – 30
⇒ 5P = 90
∴ P = Rs. 18