Syllogism

Syllogism

Easy Questions
Moderate Questions
Difficult Questions
Syllogism Tutorial

Verbal Reasoning

Eligibility Test
Logical order of words
Mathematical operation and symbol notation
Clock and calender
Problem Based on ages
Alphabet Test
Input Output
Linear Arrangement
Matrix Arrangement
Circular Arrangement
Logical Connectivity
Games And Tournament
Analogy
Classification
Number Series
Letter and Symbol Series
Coding Decoding
Sequencing and Formation
Direction and Distance
Sitting Arrangement
Blood Relations
Logical Venn Diagram
Cubes
Logical Problems
Theme Detection
Logical Deduction
Matching Definitions
Making Judgments
Logical Games
Verification of Truth/Lie of Statements
Routes and Networks
Time Sequence
Ranking Test
Inserting and Missing Character
Grid and Matrices
Syllogism
Statement and Argument
Statement and Assumption
Statement and Courses of Action
Statement and Conclusion
Cause and Effect
Grouping and Team Formation
Assertion and Reason
Situation Reaction Test
  1. For the Venn diagram given below, which of the following conclusion(s) is/are true?
    I. Some Captains are painters.
    II. Some Lieutenants are painters.
    III. All Majors are soldiers.
    IV. All Captains are soldiers.
    V. All soldiers are painters.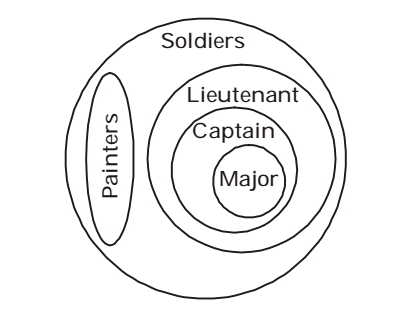










  1. View Hint View Answer Discuss in Forum

    All Majors are captains.
    All Majors are Lieutenants.
    All Majors are Soldiers.
    (This is Conclusion III )
    All captains are Soldiers.

    Correct Option: D

    All Majors are captains.
    All Majors are Lieutenants.
    All Majors are Soldiers.
    (This is Conclusion III )
    All captains are Soldiers.
    (This is Conclusion IV ).
    All Lieutenants are Soldiers.
    All Painters are Soldiers.
    No Painter is Captain.

Direction: Two statement are given followed by two conclusions I and II. You have to consider the two statements to be true even if they seem to be at variance from commonly known facts. You have to decide which one of the given conclusions are definitely drawn from the given statements:

  1. Statements :
    Some peons are poor.
    X is poor.
    Conclusions :
    I. X is a peon.
    II. X has a large family.








  1. View Hint View Answer Discuss in Forum

    The first premise is particular Affirmative (I- Type). The second premise is Universal Affirmative (A-Type).
    We can align the premises by converting the first premise and changing their order.

    Correct Option: D

    The first premise is particular Affirmative (I- Type). The second premise is Universal Affirmative (A-Type).
    We can align the premises by converting the first premise and changing their order. Thus,
    X is poor → Some poors are peons have a doctorate degree.
    We know that,
    A + I = No conclusion.

Direction: A statement(s) is/ are given followed by two conclusions I and II. You have to consider the statement(s) to be true, even if it seems to be at variance from commonly known facts. You are to decide which of the given conclusions can definitely be drawn from the given statement (s). Indicate your answer.

  1. Statements:
    (A) All basketball players are tall men.
    (B). All basketball players are athletes.
    Conclusions:
    I. All tall men are basketball players.
    II. All athletes are basketball players.








  1. View Hint View Answer Discuss in Forum

    Both the Premises are Universal Affirmative (A-type). We can align the Premises by taking converse of any of the premises.
    Some tall men are basketball players ↔ All basketball players are athletes.

    Correct Option: C

    Both the Premises are Universal Affirmative (A-type). We can align the Premises by taking converse of any of the premises.
    Some tall men are basketball players ↔ All basketball players are athletes.
    I + A ⇒I - type of conclusion ”Some tall men are athletes".

Direction: Which alternatives applies to the given statements and its conclusions?

  1. Statements:
    Some doctors are teachers.
    All teachers are counsellors.
    Conclusions:
    I. Some counsellors are not teachers.
    II. Some doctors are counsellors








  1. View Hint View Answer Discuss in Forum

    First premise is Particular Affirmative (I–type).
    Second premise is Universal Affirmative (I-type).
    Both the premises are already aligned.Thus,
    Some doctors are teachers ↔ All teachers are counsellors.

    Correct Option: B

    First premise is Particular Affirmative (I–type).
    Second premise is Universal Affirmative (I-type).
    Both the premises are already aligned. Thus,
    Some doctors are teachers ↔ All teachers are counsellors.
    We know that, I + A ⇒ I-type conclusion.
    Therefor, our derived conclusion would be:
    “Some doctors are counsellors”. Thus, only conclusion II follows.


Direction: Two statements are followed by two conclusions I and II. You have to consider the two statements to be true even if they seem to be at variance from commonly known facts. You have to decide which one of the given conclusions are definitely drawn from the given statements:

  1. Statement:
    (a) All politicians are intelligent
    (b) Some women are politicians
    Conclusions:
    I. Some women are intelligent
    II. All those intelligent are women.








  1. View Hint View Answer Discuss in Forum

    Some women are politicians. ↔ All politicians are intelligents.

    Correct Option: A

    Some women are politicians. ↔ All politicians are intelligents.
    We know that,
    I + A ⇒I–type Conclusion Thus, our derived Conclusion would be: “Some women are intelligent”.