Games And Tournament
Direction: 16 teams have been invited to participate in the ABC Gold Cup cricket tournament. The tournament is conducted in 2 stages. In the first stage, the teams are divided into two groups. Each group consists of 8 teams, with each team playing every other team in its group exactly once. At the end of the first stage, the top 4 teams from each group advance to the 2nd stage while the rest are eliminated. The second stage comprises of several rounds. A round involves one match for each team. The winner of a match in a round advances to the next round, while the loser is eliminated. The team that remains undefeated in the second stage is declared the winner and claims the Gold Cup. The tournament rules are such that each match results in a winner and a loser with no possibility of a tie. In the first stage a team earns 1 point for each win and no points for a loss. At the end of the first stage teams in each group are ranked on the basis of total points to determine the qualifiers advancing to the next stage. Ties are resolved by a series of complex tie-breaking rules so that exactly 4 teams from each group advance to the next stage.
- The minimum number of wins needed for a team in the first stage to guarantee is advancement to the next stage is:
-
View Hint View Answer Discuss in Forum
From the given information we can complete the following table it is clear that if a team wins 5 games, then also there is no guarantee of its advancement to the next stage, since only 4 teams can go to the next stage.
Correct Option: D
From the given information we can complete the following table it is clear that if a team wins 5 games, then also there is no guarantee of its advancement to the next stage, since only 4 teams can go to the next stage.
Note: In the table W → Wins, L → Loose, × → No match (as example there can not be match between 1& and 1, 2 and 2 and so on)
The above is one of such combination. Since after winning 5 matches too, there is no guarantee to advancement, so the answer must be 6, because no two teams can get 7 points each.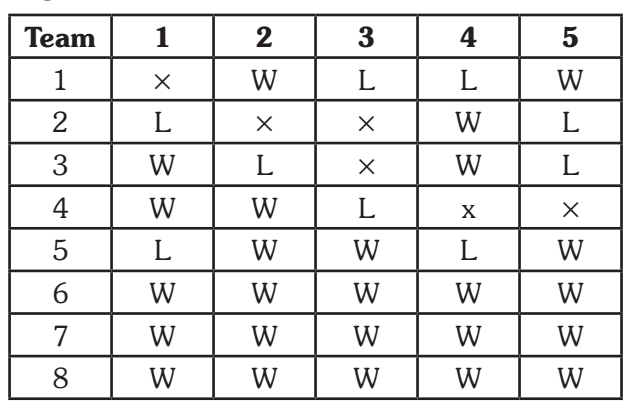
Direction: Kolkata Premier League has 16 players seeded from 1 to 16. These players are divided in 4 groups namely South Kolkata, North Kolkata, Central Kolkata and Saltlake. 16 players are divided in these groups as follows :-
South Kolkata : 1, 8, 9, 16
North Kolkata : 2, 7, 10, 15
Central Kolkata : 3, 6, 11, 14
Saltlake : 4, 5, 12,13
In stage I :, each player in a group plays with all the other members in their group exactly once. 2 from each group is selected for stage II based on their number of points. A player qualifying for stage II carries forward only those points that he gained stage I against the another player who qualifies for stage II.
In stage II :, total 8 players (2 from each group) advanced to stage II, where each player plays every other player except the player from same group. At the end of stage II, the top 4 players on the basis of points would qualify for the IIIrd stage the Semi-Final stage.
Stage III : (Semi-Final), winners of the Semi-Final advanced to the final round and losers play for 3rd place. The following more rules of tournament is as follows :
(i) Points in stage I and stage II are awarded as follows : winner 2 points, looser 0 points.
(ii) An ‘upset’ is caused when, in any match a lower seeded player beats a higher seeded player.
(iii) There is no ties at any stage.
(iv) If points of the two players at the end of any stage are same then there is a complex rule to calculate the tie breaker.
(v) Seed 1 is the highest seed and seed 16 is the lowest rank seed.
- If Ricky Singh a lucky player from South Kolkata reached semi final stage after getting the minimum possible points, then what is the point scored by Mr. Ricky Singh.
-
View Hint View Answer Discuss in Forum
In stage I, in a group in total 6 matches and that will have 12 points in total.
Total number of matches in this stage is 4 × 6 = 24
In stage II, total 8 players and they play each other except a player who comes from same group but point of their match in stage I is carried forward hence in stage II total points is 28 × 2 = 56.
Number of matches in stage II is 7 × ( 8/2 ) – 4 = 24Correct Option: A
In stage I, in a group in total 6 matches and that will have 12 points in total.
Total number of matches in this stage is 4 × 6 = 24
In stage II, total 8 players and they play each other except a player who comes from same group but point of their match in stage I is carried forward hence in stage II total points is 28 × 2 = 56.
Number of matches in stage II is 7 × ( 8/2 ) – 4 = 24
In this case we have to minimize the points scored by 4th ranker (Who advanced to Semi Final). In order to minimize the points scored by Ricky Singh top three players should get maximum points, Let points achieved by top three player at the end of stage II is 14, 12 and 10 summing up to 14 + 12 + 10 = 36 and remaining points 56 - 36 = 20 got distributed to bottom 5 players.
To minimize the points scored by Ricky Singh, all of the bottom five got same point (20/5 = 4 points) and with complex tie breaker Ricky is advanced to Semifinal.
- If Ricky Singh a lucky player from South Kolkata aspire to play semi final stage what is the minimum points he should aim to guarantee a seat in semifinal?
-
View Hint View Answer Discuss in Forum
In stage I, in a group in total 6 matches and that will have 12 points in total.
Total number of matches in this stage is 4 × 6 = 24
In stage II, total 8 players and they play each other except a player who comes from same group but point of their match in stage I is carried forward hence in stage II total points is 28 × 2 = 56.
Number of matches in stage II is 7 × ( 8/2 ) – 4 = 24Correct Option: C
In stage I, in a group in total 6 matches and that will have 12 points in total.
Total number of matches in this stage is 4 × 6 = 24
In stage II, total 8 players and they play each other except a player who comes from same group but point of their match in stage I is carried forward hence in stage II total points is 28 × 2 = 56.
Number of matches in stage II is 7 × ( 8/2 ) – 4 = 24
In stage 2 total points are 56.
Consider bottom 3 players, they must play three matches among themselves and hence they have minimum 6 points with them,
Remaining points 56 - 6 = 50 if equally divided between top 5 then one would get 10 points, so to guarantee a seat in semifinal Ricky Singh has to score 12 points .
- If there is no upset in stage 1 then the lowest seeded player who can win the tournament is -
-
View Hint View Answer Discuss in Forum
In stage I, in a group in total 6 matches and that will have 12 points in total.
Total number of matches in this stage is 4 × 6 = 24
In stage II, total 8 players and they play each other except a player who comes from same group but point of their match in stage I is carried forward hence in stage II total points is 28 × 2 = 56.
Number of matches in stage II is 7 × ( 8/2 ) – 4 = 24Correct Option: B
In stage I, in a group in total 6 matches and that will have 12 points in total.
Total number of matches in this stage is 4 × 6 = 24
In stage II, total 8 players and they play each other except a player who comes from same group but point of their match in stage I is carried forward hence in stage II total points is 28 × 2 = 56.
Number of matches in stage II is 7 × ( 8/2 ) – 4 = 24
In stage 1 a player has to win minimum 1 match to advance to the next stage.
Now consider the different groups,
South Kolkata : 1, 8, 9, 16 [seed 9 can advance after beating seed 16 without an upset]
North Kolkata : 2, 7, 10, 15 [seed 10 can advance after beating seed 15 without an upset]
Central Kolkata : 3, 6, 11, 14 [seed 11 can advance after beating seed 14 without an upset]
Saltlake : 4, 5, 12,13 [seed 12 can advance after beating seed 113 without an upset] So seed 12 is the lowest seed who can advance to stage II without causing Upset in stage I, and can win the tournament [Please note here that in stage II or semifinal there may be an Upset
Direction: 16 teams have been invited to participate in the ABC Gold Cup cricket tournament. The tournament is conducted in 2 stages. In the first stage, the teams are divided into two groups. Each group consists of 8 teams, with each team playing every other team in its group exactly once. At the end of the first stage, the top 4 teams from each group advance to the 2nd stage while the rest are eliminated. The second stage comprises of several rounds. A round involves one match for each team. The winner of a match in a round advances to the next round, while the loser is eliminated. The team that remains undefeated in the second stage is declared the winner and claims the Gold Cup. The tournament rules are such that each match results in a winner and a loser with no possibility of a tie. In the first stage a team earns 1 point for each win and no points for a loss. At the end of the first stage teams in each group are ranked on the basis of total points to determine the qualifiers advancing to the next stage. Ties are resolved by a series of complex tie-breaking rules so that exactly 4 teams from each group advance to the next stage.
- What is the total number of matches played in the tournament?
-
View Hint View Answer Discuss in Forum
First Stage: There is two groups of 8 teams each. In each group, each team plays with every other team and hence total number of matches are 8c2 = 8 × ( 7/2 ) = 28 matches So, in both the groups the total number of matches played at the first stage are 28. And hence 56 matches are played in 1st stage
Second Stage: In this stage there are 8 teams playing in such a way that in one round 4 teams play with 4 other teams. 4 teams win and go to the next round. That is called knock out tournament.Correct Option: C
First Stage: There is two groups of 8 teams each. In each group, each team plays with every other team and hence total number of matches are 8c2 = 8 × ( 7/2 ) = 28 matches So, in both the groups the total number of matches played at the first stage are 28. And hence 56 matches are played in 1st stage
Second Stage: In this stage there are 8 teams playing in such a way that in one round 4 teams play with 4 other teams. 4 teams win and go to the next round. That is called knock out tournament.
In the 1st round no of matches ( 8/2 ) = 4,
In the 2nd round no of matches = ( 4/2 ) = 2,
In the third or the last round number of match = ( 2/2 ) = 1,
So , total no. of matches in 2nd stage is 4 + 2 + 1 = 7
Hence total match in the tournament = 56 + 7 = 63

