Network theory miscellaneous

Network theory miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Network Theory

Network Elements and the Concept of Circuit
Network theory miscellaneous
  1. Consider the circuit as shown below which has a current dependent current source. The value V2 /V1 is—










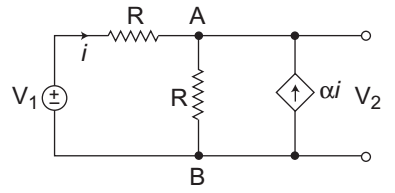
  1. View Hint View Answer Discuss in Forum

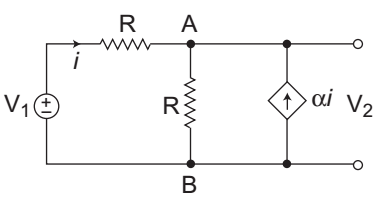
    The given circuit:

    Applying KCL at node A, we get

    VA - V1
    		 +
    VA
    		= αi ........…(i)
    RR

    From figure:
    VA = V2 and
    V1 - VA
    		= i
    R

    Now,
    V2 - V1
    		 +
    V2
    		= α
    V1 - VA
    		 = i
    RRR

    or
    V2
    1
    		 +
    1
    		 +
    α
    		=
    α
    		 V1 +
    V1
    RRRRR

    or
    V2
    2 + α
    		 = V1
    α + 1
    RR

    or
    V2
    		 =
    1 + α
    V12 + α

    Hence alternative (C) is the correct choice.

    Correct Option: C

    The given circuit:

    Applying KCL at node A, we get

    VA - V1
    		 +
    VA
    		= αi ........…(i)
    RR

    From figure:
    VA = V2 and
    V1 - VA
    		= i
    R

    Now,
    V2 - V1
    		 +
    V2
    		= α
    V1 - VA
    		 = i
    RRR

    or
    V2
    1
    		 +
    1
    		 +
    α
    		=
    α
    		 V1 +
    V1
    RRRRR

    or
    V2
    2 + α
    		 = V1
    α + 1
    RR

    or
    V2
    		 =
    1 + α
    V12 + α

    Hence alternative (C) is the correct choice.

  1. The laplace transform of the waveform shown in the figure is
    F(s) =
    1
    		 (1 + Ae-e + Be-4s + Ce-6s + De-8s)
    s2

    What is the value of D?










  1. View Hint View Answer Discuss in Forum

    The given waveform:

    Given, F(s) =
    1
    		[1 + Ae–s + Be–4s + Ce–6s + De–8s]
    s2

    The slope of D is 1/2 = 0·5
    Hence alternative (C) is the correct choice.

    Correct Option: C

    The given waveform:

    Given, F(s) =
    1
    		[1 + Ae–s + Be–4s + Ce–6s + De–8s]
    s2

    The slope of D is 1/2 = 0·5
    Hence alternative (C) is the correct choice.

  1. Which one of the following is the transfer function of an electrical low pass filter using R and C elements?








  1. View Hint View Answer Discuss in Forum

    The low pass filter using R and C components:

    V0(s) =Vi(s)
    1
    Cs
    R +
    1
    Cs

    V0(s)
    		= H(s) =
    1
    Vi(s)(1 + RCs)

    Hence alternative (B) is the correct choice.

    Correct Option: B

    The low pass filter using R and C components:

    V0(s) =Vi(s)
    1
    Cs
    R +
    1
    Cs

    V0(s)
    		= H(s) =
    1
    Vi(s)(1 + RCs)

    Hence alternative (B) is the correct choice.

  1. In the circuit shown in the figure below, for what value of C will the current I be in phase with the sinusoidal source voltage Vs = sin 2t?










  1. View Hint View Answer Discuss in Forum

    The given circuit:

    Given, Vs = sin 2t, means = 2 rad/sec.
    In order to make the current I in phase with the sinusoidal source voltage, the imaginary part of the net impedance offered by the voltage source must be zero.
    So,

    Zeq =
    1
    		|| (1 + j1)
    j C

    or
    Zeq =
    1
    		× (1 + j)
    j2C
    1
    		 + (1 + j)
    j2C

    or
    Zeq =
    1
    		× [1 + j]
    2C
    2C + j (2C - 1)

    2C – 1 = 0 (Since Imaginary part must be zero)
    or
    C = 1/2 F
    Hence alternative (B) is the correct choice.

    Correct Option: B

    The given circuit:

    Given, Vs = sin 2t, means = 2 rad/sec.
    In order to make the current I in phase with the sinusoidal source voltage, the imaginary part of the net impedance offered by the voltage source must be zero.
    So,

    Zeq =
    1
    		|| (1 + j1)
    j C

    or
    Zeq =
    1
    		× (1 + j)
    j2C
    1
    		 + (1 + j)
    j2C

    or
    Zeq =
    1
    		× [1 + j]
    2C
    2C + j (2C - 1)

    2C – 1 = 0 (Since Imaginary part must be zero)
    or
    C = 1/2 F
    Hence alternative (B) is the correct choice.

  1. In the circuit shown below, what is the voltage across 5Ω resistor i.e. (V1 – V2)










  1. View Hint View Answer Discuss in Forum

    The given circuit:

    From figure, KCL at node 1

    V1
    		 +
    V1 – V2
    		 = 176 …. .......(i)
    75

    Again KCL at node 2
    V2
    		 +
    V2 – V1
    		 = 110 …. .......(i)
    105

    From equation (i) and (ii), we get
    V1 = 1190V and V2 = 1160V
    Now, V1 – V2 = 1190 – 1160 = 30V

    Correct Option: B

    The given circuit:

    From figure, KCL at node 1

    V1
    		 +
    V1 – V2
    		 = 176 …. .......(i)
    75

    Again KCL at node 2
    V2
    		 +
    V2 – V1
    		 = 110 …. .......(i)
    105

    From equation (i) and (ii), we get
    V1 = 1190V and V2 = 1160V
    Now, V1 – V2 = 1190 – 1160 = 30V