46. For the circuit shown below, the current supplied by the sinusoidal current source I is—
    
    
    
    

1. 1. 28A
      

   
   
   

   2. 4A
      

   
   
   

   3. 20A
      

   
   
   

   4. Not determinable from the given data

   
   
   

---

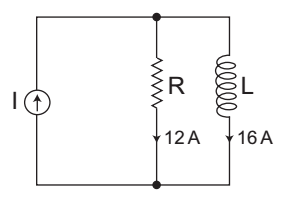
1. View Hint View Answer Discuss in Forum

   The given circuit:
   
   The current supplied sinusoidal current source
   I = I_R² + I_L²
   or
   I = 12² + 16² = 144 + 256
   = 400 = 20A.

   Correct Option: C

   The given circuit:
   
   The current supplied sinusoidal current source
   I = I_R² + I_L²
   or
   I = 12² + 16² = 144 + 256
   = 400 = 20A.

---

47. The phase angle of the circuit—
    

1. 1. 33°
      

   
   
   

   2. – 33°
      

   
   
   

   3. – 33·6°
      

   
   
   

   4. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Phase angle,
   

   φ = tan–1	XC
   	R

   
   or
   

   φ = tan–1	0·126	= 33°
   	0·2

   Correct Option: A

   Phase angle,
   

   φ = tan–1	XC
   	R

   
   or
   

   φ = tan–1	0·126	= 33°
   	0·2

---

---

48. The total impedance of the circuit—
    

1. 1. 83·3 ∠ 33°Ω
      

   
   
   

   2. 83·3 ∠ – 33°Ω
      

   
   
   

   3. 38·3 ∠ – 33°Ω
      

   
   
   

   4. None of these

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Total impedance of the circuit,
   

   ZT =	Vs	=	20     0°
   	IT		0·24 × 33°

   
   = 83.3 -33°Ω
   

   Correct Option: B

   Total impedance of the circuit,
   

   ZT =	Vs	=	20     0°
   	IT		0·24 × 33°

   
   = 83.3 -33°Ω
   

---

49. The phase angle for the circuit shown below is—
    
    
    
    

1. 1. 47·7°
      

   
   
   

   2. – 47·7°
      

   
   
   

   3. – 37·8°
      

   
   
   

   4. 38·8°

   
   
   

---

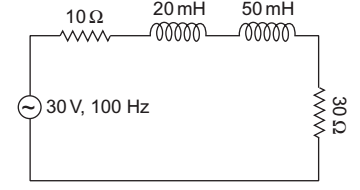
1. View Hint View Answer Discuss in Forum

   The given circuit:
   
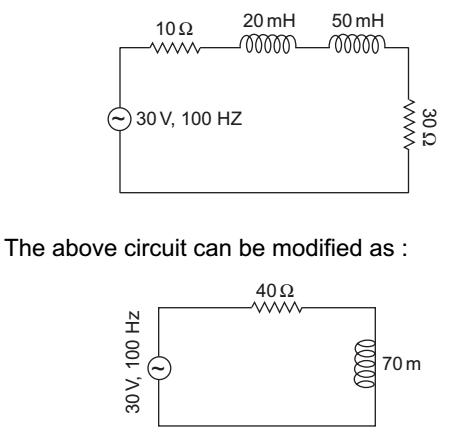
   From above circuit,
   X_L = 2πf L = 2 × 3·14 × 100 × 70 × 10^–3
   = 43·98Ω
   Now,
   Z_eq = (40 + j43·98)Ω
   Current,
   

   I =	Vs	=	30 0°
   	Zeq		40 + j43·98

   
   ≈ 0·5 – 47·7°A
   Thus, we conclude that current lags behind the applied voltage by 47·7°. Hence the phase angle between voltage and current, θ = 47·7°.

   Correct Option: A

   The given circuit:
   
   From above circuit,
   X_L = 2πf L = 2 × 3·14 × 100 × 70 × 10^–3
   = 43·98Ω
   Now,
   Z_eq = (40 + j43·98)Ω
   Current,
   

   I =	Vs	=	30 0°
   	Zeq		40 + j43·98

   
   ≈ 0·5 – 47·7°A
   Thus, we conclude that current lags behind the applied voltage by 47·7°. Hence the phase angle between voltage and current, θ = 47·7°.

---

---

50. The given circuit is a combination of—
    
    
    
    

1. 1. resistance of 2·4Ω in series with capacitive reactance 2·8Ω
      

   
   
   

   2. resistance of 2·4Ω in series with capacitive reactance 2·4Ω
      

   
   
   

   3. resistance of 2·8Ω in series with capacitive reactance 2·4Ω
      

   
   
   

   4. resistance of 2·4Ω in parallel with capacitive reactance 2·8Ω

   
   
   

---

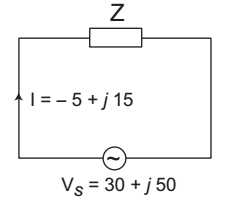
1. View Hint View Answer Discuss in Forum

   The given circuit:
   
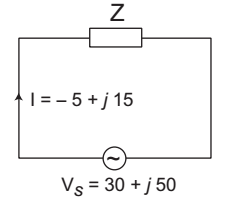
   The impedance of the given circuit
   

   Z =	30 + j50	=	30   0°	=	58·31   59°
   	I		– 5 + j15		15·81 – 108·43°

   
   = 3·69 – 49·43° or Z = (2·4 – j 2·8)Ω
   Therefore, the circuit has a resistance of 2·4Ω in series with capacitive reactance 2·8Ω.

   Correct Option: A

   The given circuit:
   
   The impedance of the given circuit
   

   Z =	30 + j50	=	30   0°	=	58·31   59°
   	I		– 5 + j15		15·81 – 108·43°

   
   = 3·69 – 49·43° or Z = (2·4 – j 2·8)Ω
   Therefore, the circuit has a resistance of 2·4Ω in series with capacitive reactance 2·8Ω.

---