Network theory miscellaneous

Network theory miscellaneous

Easy Questions
Moderate Questions
Difficult Questions

Network Theory

Network Elements and the Concept of Circuit
Network theory miscellaneous
  1. Which one of the following is the transmission matrix for the network shown in the figure given above?
    1
    1+yz
    yz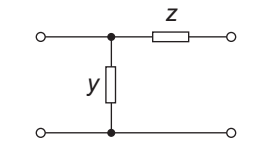










  1. View Hint View Answer Discuss in Forum

    The given figure:

    The transmission matrix is given by:

    V1
    		 =
    V2
    A
    B
    l1-l2CD

    V1 = AV2 – BI2 . . . …(i)
    and I1 = CV2 – DI2 . . .…(ii)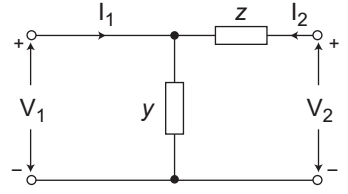

    From figure:
    V1 = (I1 + I2) × 1/y
    and
    V2 = I2z +
    I1 + I2
    		= l2z +
    I1
    		 +
    I2
    yyy

    or
    I1 = – I2 (1 + yz) + V2y . . . . .…(iii)
    and V1 = – I2z + V2 …. . . . .(iv)
    On comparing equation (i) and (ii) with (iii) and (iv), we get:
    A
    B
    		 =
    1
    z
    CDy1+yz

    Hence alternative (C) is the correct choice.

    Correct Option: C

    The given figure:

    The transmission matrix is given by:

    V1
    		 =
    V2
    A
    B
    l1-l2CD

    V1 = AV2 – BI2 . . . …(i)
    and I1 = CV2 – DI2 . . .…(ii)

    From figure:
    V1 = (I1 + I2) × 1/y
    and
    V2 = I2z +
    I1 + I2
    		= l2z +
    I1
    		 +
    I2
    yyy

    or
    I1 = – I2 (1 + yz) + V2y . . . . .…(iii)
    and V1 = – I2z + V2 …. . . . .(iv)
    On comparing equation (i) and (ii) with (iii) and (iv), we get:
    A
    B
    		 =
    1
    z
    CDy1+yz

    Hence alternative (C) is the correct choice.

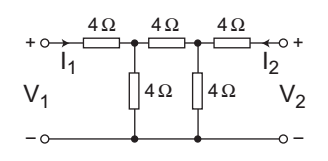
  1. What is the value of the parameter h12 for the 2-port network shown in the figure given above?










  1. View Hint View Answer Discuss in Forum

    The given network

    We know that

    h12 =
    V1
    		/I1 = 0
    V2

    The given network can be modified as:

    Applying KCL at node A
    VA- V2
    		+
    VA
    		+
    VA- V1
    		= 0
    484

    or
    VA
    1
    		+
    1
    		+
    1
    		=
    V2
    		+
    V1
    48444

    or
    5
    		VA =
    V2
    		+
    V1
    844

    or
    5
    		VA = V2 + V1 …. . . . . . (i)
    2

    Again by applying potential divider rule
    V1 = V1 ×
    4
    		 =
    VA
    22

    or
    VA = 2V1
    Now
    5
    		.2V1 = V2 + V1
    2

    or
    4 V1 = V2
    or
    V1
    		 =
    1
    		 = h12 = 0·250Ω
    V24

    Hence alternative (C) is the correct choice.

    Correct Option: C

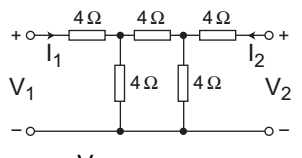
    The given network

    We know that

    h12 =
    V1
    		/I1 = 0
    V2

    The given network can be modified as:

    Applying KCL at node A
    VA- V2
    		+
    VA
    		+
    VA- V1
    		= 0
    484

    or
    VA
    1
    		+
    1
    		+
    1
    		=
    V2
    		+
    V1
    48444

    or
    5
    		VA =
    V2
    		+
    V1
    844

    or
    5
    		VA = V2 + V1 …. . . . . . (i)
    2

    Again by applying potential divider rule
    V1 = V1 ×
    4
    		 =
    VA
    22

    or
    VA = 2V1
    Now
    5
    		.2V1 = V2 + V1
    2

    or
    4 V1 = V2
    or
    V1
    		 =
    1
    		 = h12 = 0·250Ω
    V24

    Hence alternative (C) is the correct choice.

  1. What is the value of R required for maximum power transfer in the network shown above?










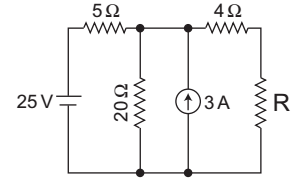
  1. View Hint View Answer Discuss in Forum

    The given network:

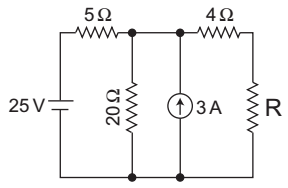
    Let R = RL.
    The value of R required for maximum power transfer in network is equivalent to net resistance as seen from the open load terminal (i.e. Thevenin’s resistance, Rth)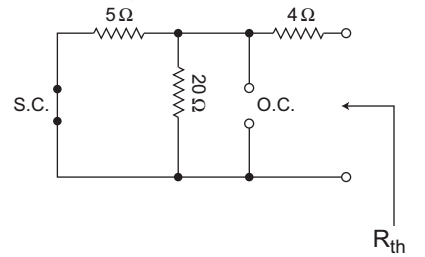

    From above figure,
    Rth = [5 || 20] + 4Ω = 4Ω + 4Ω = 8Ω
    Hence alternative (C) is the correct choice

    Correct Option: C

    The given network:

    Let R = RL.
    The value of R required for maximum power transfer in network is equivalent to net resistance as seen from the open load terminal (i.e. Thevenin’s resistance, Rth)

    From above figure,
    Rth = [5 || 20] + 4Ω = 4Ω + 4Ω = 8Ω
    Hence alternative (C) is the correct choice

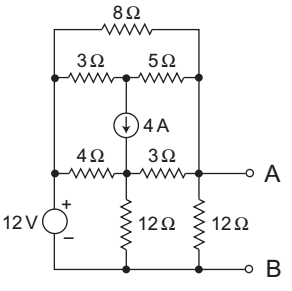
  1. What is the Thevenin resistance seen from the terminals AB of the circuit shown above in the figure?










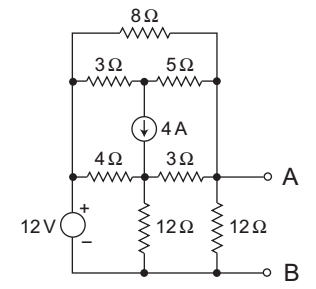
  1. View Hint View Answer Discuss in Forum

    The given circuit:

    The equivalent circuit for calculation of Rth is shown below—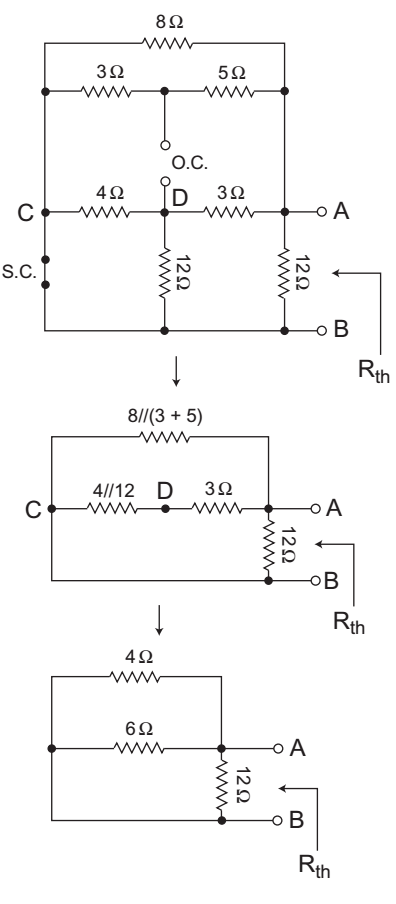

    Now, from above figure

    1
    		 =
    1
    		 +
    1
    		 +
    1
    Rth4612

    or
    1
    		 =
    3 + 2 + 1
    Rth12

    or
    Rth =
    12
    		 = 2Ω
    6

    Hence alternative (A) is the correct choice.

    Correct Option: A

    The given circuit:

    The equivalent circuit for calculation of Rth is shown below—

    Now, from above figure

    1
    		 =
    1
    		 +
    1
    		 +
    1
    Rth4612

    or
    1
    		 =
    3 + 2 + 1
    Rth12

    or
    Rth =
    12
    		 = 2Ω
    6

    Hence alternative (A) is the correct choice.

  1. The circuit shown in the above figure
    1. is reciprocal
    2. has Z11 = 2, Z22 = 2
    3. has Z11 = 4, Z22 = 2
    4. has Z11 = 0, Z22 = 2
    Select the correct answer using the code given below—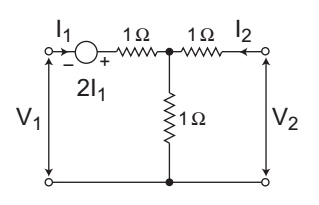










  1. View Hint View Answer Discuss in Forum

    The given circuit:

    Applying KVL in the input side, we get
    V1 = 2I1 + I1.1 + (I1 + I2).1
    or
    V1 = 4I1 + I2 …. . . .(i)
    Again applying KVL in the output side, we get
    V2 = I2.1 + (I1 + I2).1
    or
    V2 = I1 + 2I2. . . . …(ii)
    From equation (i) and (ii):
    Z11 = 4Ω, Z12 = 1Ω
    Z21 = 1Ω, Z22 = 2Ω
    For the network to be reciprocal
    Z12 = Z21 (Here Z11 = Z12 = 1Ω)
    So, network is reciprocal
    and
    Z11 = 4Ω, Z22 = 2Ω
    Therefore, statements 1 and 3 are correct.
    Hence alternative (A) is the correct choice.

    Correct Option: A

    The given circuit:

    Applying KVL in the input side, we get
    V1 = 2I1 + I1.1 + (I1 + I2).1
    or
    V1 = 4I1 + I2 …. . . .(i)
    Again applying KVL in the output side, we get
    V2 = I2.1 + (I1 + I2).1
    or
    V2 = I1 + 2I2. . . . …(ii)
    From equation (i) and (ii):
    Z11 = 4Ω, Z12 = 1Ω
    Z21 = 1Ω, Z22 = 2Ω
    For the network to be reciprocal
    Z12 = Z21 (Here Z11 = Z12 = 1Ω)
    So, network is reciprocal
    and
    Z11 = 4Ω, Z22 = 2Ω
    Therefore, statements 1 and 3 are correct.
    Hence alternative (A) is the correct choice.