Network theory miscellaneous Moderate Questions and Answers | Page - 13

Network theory miscellaneous

For the given network, the current I is—

1. 2A
1. 5A
1. 7A
1. 9A

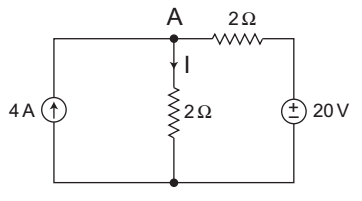
View Hint View Answer Discuss in Forum

The given circuit:

KCL at node A
4 = V_A + V_{A - 20}
2 2

ro
V_A + V_A = 4 + 10
2 2

or
V_A = 14V
Now,
I = V_A + 14 = 7A
2 2

Correct Option: C

The given circuit:

KCL at node A
4 = V_A + V_{A - 20}
2 2

ro
V_A + V_A = 4 + 10
2 2

or
V_A = 14V
Now,
I = V_A + 14 = 7A
2 2

Which one of the following parameters does not exist for the two-port network shown in the given figure—

1. ABCD
1. Y
1. h
1. Z

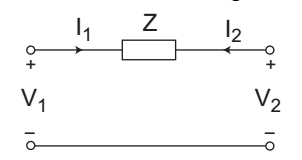
View Hint View Answer Discuss in Forum

The Z-parameters does not exist for the given twoport network.

Correct Option: D

The Z-parameters does not exist for the given twoport network.

The two electrical subnetworks N₁ and N₂ are connected through three resistors as shown below. The voltage across the 5Ω resistor and the 1Ω resistor are given to be 10V and 5V respectively. The voltage across the 15Ω resistor is—

1. – 105V
1. + 105V
1. – 15V
1. + 15V

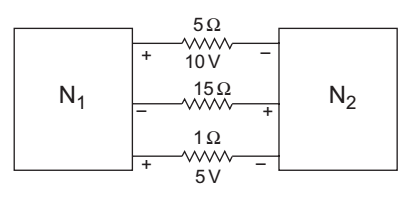
View Hint View Answer Discuss in Forum

The given circuit

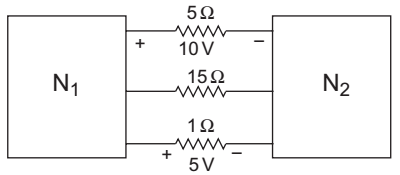
Current in 5Ω resistor
l₁ = 10 = 2A(From N₁ to N₂)
5

Current in 1Ω resistor
I₂ = 5/1 = 5A (From N₁ to N₂)
The current in 15Ω resistor must be = 2 + 5 = 7A (from N₂ to N₁)
The voltage across 15Ω resistor = – 15 × 7V = – 105V.

Correct Option: A

The given circuit

Current in 5Ω resistor
l₁ = 10 = 2A(From N₁ to N₂)
5

Current in 1Ω resistor
I₂ = 5/1 = 5A (From N₁ to N₂)
The current in 15Ω resistor must be = 2 + 5 = 7A (from N₂ to N₁)
The voltage across 15Ω resistor = – 15 × 7V = – 105V.

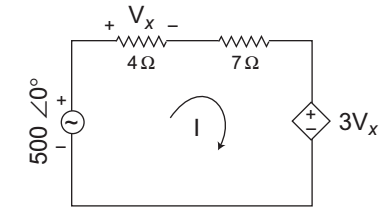
The average power delivered by the 500 ∠ 0° voltage source and dependent source for the circuit shown below—

1. 5·432 kW, – 2·833 kW
1. 54·32 kW, – 2·833 kW
1. 28·33 kW, 5·432 kW
1. 2·833 kW, – 5·432 kW

View Hint View Answer Discuss in Forum

The given circuit:

From given circuit 5
00 0° – 4I – 7I – 3V_x = 0 . . . . …(i)
and
V_x = 4I . . . . …(ii)
From equation (i) and (ii) 500 0° – 11I – 3V_x = 0
or 500 – 11I – 3 × 4 I= 0
or
I = 500   0° = 21·73   0°
23

Now, the power delivered by the 500 0° voltage source =
1/2 VI
= 1 × 500   0°× 21·73
2

= 5·432kW
The power delivered by the independent voltage source
= 1 3V_x × I = 1 × 3 × 4I × I
2 2

= 6I² = 6 (21·73)²
= 2·833 kW
Since the current I entering therefore power delivered will be negative i.e. – 2·833 kW.
Hence alternative (A) is the correct choice.

Correct Option: A

The given circuit:

From given circuit 5
00 0° – 4I – 7I – 3V_x = 0 . . . . …(i)
and
V_x = 4I . . . . …(ii)
From equation (i) and (ii) 500 0° – 11I – 3V_x = 0
or 500 – 11I – 3 × 4 I= 0
or
I = 500   0° = 21·73   0°
23

Now, the power delivered by the 500 0° voltage source =
1/2 VI
= 1 × 500   0°× 21·73
2

= 5·432kW
The power delivered by the independent voltage source
= 1 3V_x × I = 1 × 3 × 4I × I
2 2

= 6I² = 6 (21·73)²
= 2·833 kW
Since the current I entering therefore power delivered will be negative i.e. – 2·833 kW.
Hence alternative (A) is the correct choice.

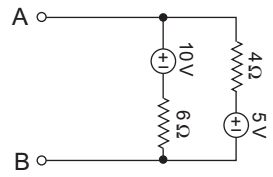
In the circuit shown below, viewed from AB, the circuit can be reduced to an equivalent circuit as—

1. 5V source in series with 10Ω resistor
1. 7V source in series with 2·4Ω resistor
1. 15V source in series with 2·4Ω resistor
1. 1V source in series with 10Ω resistor

View Hint View Answer Discuss in Forum

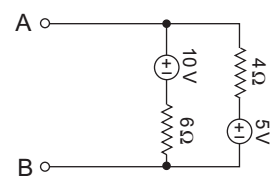
The given circuit:

Equivalent circuit for R_th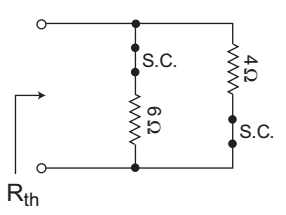

From figure, R_th = 4|| 6 = 2·4Ω
V_th = 10 – 6 I
where,
l = 10 - 5 = 5 = 0.5A
6 + 4 10

Now,
V_th = 10 – 6 × 0·5 = 10 – 3 = 7V

Correct Option: B

The given circuit:

Equivalent circuit for R_th

From figure, R_th = 4|| 6 = 2·4Ω
V_th = 10 – 6 I
where,
l = 10 - 5 = 5 = 0.5A
6 + 4 10

Now,
V_th = 10 – 6 × 0·5 = 10 – 3 = 7V