141. The maximum tensile stress at the section X-X shown in the figure below is
     

1. 1. 8P/bd

   
   
   

   2. 6P/bd

   
   
   

   3. 4P/bd

   
   
   

   4. 2P/bd

   
   
   

---

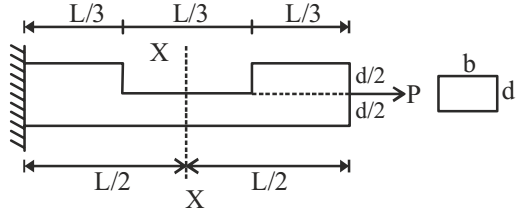
1. View Hint View Answer Discuss in Forum

   
   

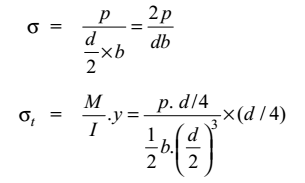
   =	6P
   	bd

   
   Max tensile stress
   

   =	2P	+	6P	=	8P
   	bd		bd		bd

   Correct Option: A

   
   

   =	6P
   	bd

   
   Max tensile stress
   

   =	2P	+	6P	=	8P
   	bd		bd		bd

---

142. The maximum shear stress in a solid shaft of circular cross-section having diameter subjected to a torque T is t. If the torque is increased by four times and the diameter of the shaft is increased by two times, the maximum shear stress in the shaft will be

1. 1. 2t

   
   
   

   2. t

   
   
   

   3. t/2

   
   
   

   4. t/4

   
   
   

---

1. View Hint View Answer Discuss in Forum

   	τ	=	T
   	r		J

   
   

   τ1	T.d/2	J =	π	d4
   	J		32

   
   

   =	Td/2
   	π	d4
   	32

   
   

   τ2 =	4T × 2d/2
   	π	(2d)4
   	32

   
   

   =	4Td
   	π	16d4
   	32

   
   

   ∴	τ2	=	1
   	τ1		2

   
   

   ∴ τ2 =	τ
   	2

   Correct Option: C

   	τ	=	T
   	r		J

   
   

   τ1	T.d/2	J =	π	d4
   	J		32

   
   

   =	Td/2
   	π	d4
   	32

   
   

   τ2 =	4T × 2d/2
   	π	(2d)4
   	32

   
   

   =	4Td
   	π	16d4
   	32

   
   

   ∴	τ2	=	1
   	τ1		2

   
   

   ∴ τ2 =	τ
   	2

---

---

143. The degree of static indeterminacy of the rigid frame having two internal hinges as shown in the figure below, is
     

1. 1. 8

   
   
   

   2. 7

   
   
   

   3. 6

   
   
   

   4. 5

   
   
   

---

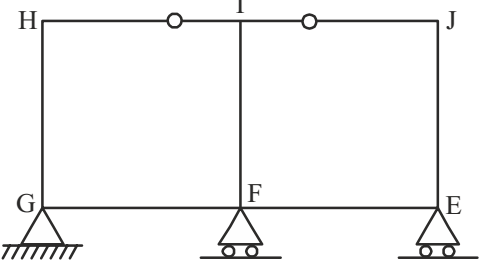
1. View Hint View Answer Discuss in Forum

   Degree of static indeterminacy
   = no. of external forces + no. of internal reaction – 3 – no. of internal hinges
   = 4 + 2 × 3 – 3 – 2 = 5

   Correct Option: D

   Degree of static indeterminacy
   = no. of external forces + no. of internal reaction – 3 – no. of internal hinges
   = 4 + 2 × 3 – 3 – 2 = 5

---

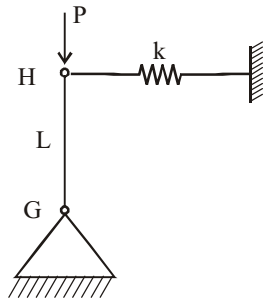
144. A rigid bar GH of length L is supported by a hinge and a spring of stiffness K as shown in the figure below. The buckling load, P_CT for the bar will be
     

1. 1. 0.5 KL

   
   
   

   2. 0.8 KL

   
   
   

   3. 1.0 KL

   
   
   

   4. 1.2 KL

   
   
   

---

1. View Hint View Answer Discuss in Forum

   Moment at G = 0 (hinge)
   At collapse, moment at G
   P_Cr × δ = k - δ × L
   ∴ P_Cr = k .L

   Correct Option: C

   Moment at G = 0 (hinge)
   At collapse, moment at G
   P_Cr × δ = k - δ × L
   ∴ P_Cr = k .L

---

---

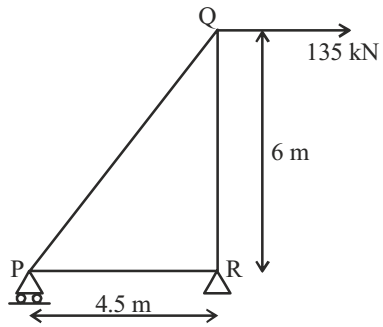
145. The right triangular truss is made of members having equal cross sectional area of 1550 mm² and Young’s modulus of 2 × 10⁵ MPa. The horizontal deflection of the joint Q is
     

1. 1. 2.47 mm

   
   
   

   2. 10.25 mm

   
   
   

   3. 14.31 mm

   
   
   

   4. 15.68 mm

   
   
   

---

1. View Hint View Answer Discuss in Forum

   ∑M_R
   = 0 135 × 6 = V_p × 4.5
   ∴ V_p = 180 kN (↓)
   ∴ V_R = 180 kN ­ ↑ (for balancing)
   At P,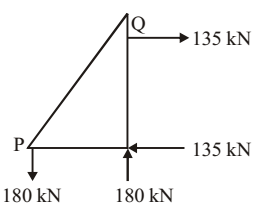
   
   F_PQ = 180 kN
   θ = tan^-1 (6/ 4.5)
   = 53.13°
   ∴ F_PQ = 225kN F_ak = 180kN
   

   δH =	∑P.L
   	AE

   
   

   =	1000
   	1550 × 2 × 105

   
   
   (Dividing by 125 to get force in each member for 1 kN force)
   we get, δH =15.68 mm

   Correct Option: D

   ∑M_R
   = 0 135 × 6 = V_p × 4.5
   ∴ V_p = 180 kN (↓)
   ∴ V_R = 180 kN ­ ↑ (for balancing)
   At P,
   
   F_PQ = 180 kN
   θ = tan^-1 (6/ 4.5)
   = 53.13°
   ∴ F_PQ = 225kN F_ak = 180kN
   

   δH =	∑P.L
   	AE

   
   

   =	1000
   	1550 × 2 × 105

   
   
   (Dividing by 125 to get force in each member for 1 kN force)
   we get, δH =15.68 mm

---