36. Match the information given in Group-I with those in Group-II.
    

    Group-I	Group-II
    P. Factor to decrease ultimate strength to design strength	1. Upper bound on ultimate load
    Q. Factor to increase working load to ultimate load for design	2. Lower bound on ultimate load
    R. Statical method of ultimate load analysis	3. Material partial safety factor
    S. Kinematical mechanism method of ultimate load analysis	4. Load factor

1. 1. P - 1; Q - 2; R - 3; S - 4

   
   
   

   2. P - 2; Q - 1; R - 4; S - 3

   
   
   

   3. P - 3; Q - 4; R - 2; S - 1

   
   
   

   4. P - 4; Q - 3; R - 2; S - 1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   P - 3; Q - 4; R - 2; S - 1

   Correct Option: C

   P - 3; Q - 4; R - 2; S - 1

---

37. The possible location of shear centre of the channel section, shown below, is
    

1. 1. P

   
   
   

   2. Q

   
   
   

   3. R

   
   
   

   4. S

   
   
   

---

1. View Hint View Answer Discuss in Forum

   NA

   Correct Option: A

   NA

---

---

38. Group I contains representative stress-strain curves as shown in the figure, while Group II gives the list of materials. Match the stress-strain curves with the corresponding materials.
    
    

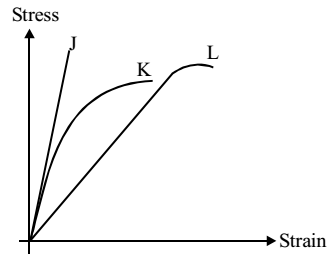
    Group-I	Group-II
    P. Curve J	1. Cement paste
    Q. Curve K	2. Coarse aggregate
    R. Curve L	3. Concrete

1. 1. P - 1; Q - 3; R - 2

   
   
   

   2. P - 2; Q - 3; R - 1

   
   
   

   3. P - 3; Q - 1; R - 2

   
   
   

   4. P - 3; Q - 2; R - 1

   
   
   

---

1. View Hint View Answer Discuss in Forum

   P - 2; Q - 3; R - 1

   Correct Option: B

   P - 2; Q - 3; R - 1

---

39. The first moment of area about the axis bending for a beam cross-section is

1. 1. moment of inertia

   
   
   

   2. section modulus

   
   
   

   3. shape factor

   
   
   

   4. polar moment of inertia

   
   
   

---

1. View Hint View Answer Discuss in Forum

   section modulus

   Correct Option: B

   section modulus

---

---

40. A cantilever beam of length L and a cross section with shape factor f supports a concentrated load P as shown below:
    
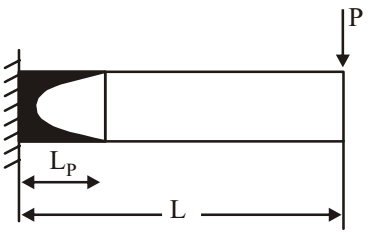
    The length L_p of the plastic zone, when the maximum bending moment, equals the plastic moment M_p, given by

1. 1. 	LP	=	1
      	L		f

   
   
   

   2. 	LP	L(1 - f)
      	L

   
   
   

   3. 	LP	=1 -	1
      	L		√f

   
   
   

   4. 	LP	=1 -	1
      	L		f

   
   
   

---

1. View Hint View Answer Discuss in Forum

   
   From similar triangles,
   

   	LP	=	L
   	MP - Me		MP

   
   

   = L		1 -	Me
   			MP

   
   

   = L		1 -	1
   			f

   
   

   ∴	LP	= 1 -	1
   	L		f

   Correct Option: D

   
   From similar triangles,
   

   	LP	=	L
   	MP - Me		MP

   
   

   = L		1 -	Me
   			MP

   
   

   = L		1 -	1
   			f

   
   

   ∴	LP	= 1 -	1
   	L		f

---