Mechanical and structural analysis miscellaneous

Mechanical and structural analysis miscellaneous

Easy Questions

Mechanics and Structural Analysis

Mechanical and structural analysis miscellaneous

Direction: A two span continuous beam having equal spans each of length L is subjected to a uniformly distributed load w per unit length. The beam has constant flexural rigidity.

  1. The bending moment at the middle support is








  1. View Hint View Answer Discuss in Forum

    RA + RB + RC = 2wL
    Let RA = RB = R
    2R = 2wL - RC

    = 2wL -
    5wL
    4

    =
    3wL
    4

    ∴ R =
    3wL
    8

    BM at C =
    3wL
    		× L -
    wL2
    82

    = -
    wL2
    2

    Correct Option: B

    RA + RB + RC = 2wL
    Let RA = RB = R
    2R = 2wL - RC

    = 2wL -
    5wL
    4

    =
    3wL
    4

    ∴ R =
    3wL
    8

    BM at C =
    3wL
    		× L -
    wL2
    82

    = -
    wL2
    2

  1. The reaction at the middle support is








  1. View Hint View Answer Discuss in Forum

    When support C is removed

    δL =
    5
    w(2L)4
    384EI

    Actual
    δL =
    R(2L)3
    48EI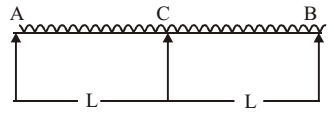


    By compatibility equation,
    5
    w × 16L4
    		=
    R × 8L3
    384EI48EI

    ∴ R =
    8wL
    4

    Correct Option: C

    When support C is removed

    δL =
    5
    w(2L)4
    384EI

    Actual
    δL =
    R(2L)3
    48EI


    By compatibility equation,
    5
    w × 16L4
    		=
    R × 8L3
    384EI48EI

    ∴ R =
    8wL
    4

Direction: Consider a propped cantilever beam ABC under two loads of magnitude P each as shown in the figure below. Flexural rigidity of the beam is EI.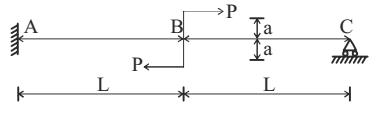

  1. The rotation at B is








  1. View Hint View Answer Discuss in Forum

    Actual rotation at B = Rotation at B due to applied force ↻ – Rotation at B due to Rc ↺.

    =
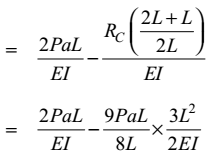
    5PaL
    		↷
    16EI

    Correct Option: A

    Actual rotation at B = Rotation at B due to applied force ↻ – Rotation at B due to Rc ↺.

    =
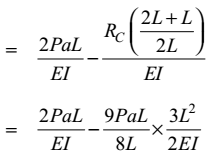
    5PaL
    		↷
    16EI

  1. The reaction at C is








  1. View Hint View Answer Discuss in Forum

    Remove support C.
    deflection (at C)

    =
    2p.a.L2
    		+
    2p.aL
    		× L
    2EIEI

    =
    3PaL2
    EI

    Deflection at C due to
    RC =
    RC × (2C)3
    3EI

    =
    RC × 8L3
    3EI

    Equating, (by compatibility equation)
    2paL2
    		=
    RC × 8L3
    EI3EI

    ⇒ RC =
    9Pa
    		↑
    8L

    Correct Option: C

    Remove support C.
    deflection (at C)

    =
    2p.a.L2
    		+
    2p.aL
    		× L
    2EIEI

    =
    3PaL2
    EI

    Deflection at C due to
    RC =
    RC × (2C)3
    3EI

    =
    RC × 8L3
    3EI

    Equating, (by compatibility equation)
    2paL2
    		=
    RC × 8L3
    EI3EI

    ⇒ RC =
    9Pa
    		↑
    8L

Direction: A truss is shown in the figure. Members are to equal cross section A and same modulus of elasticity E. A vertical force P is applied at point C.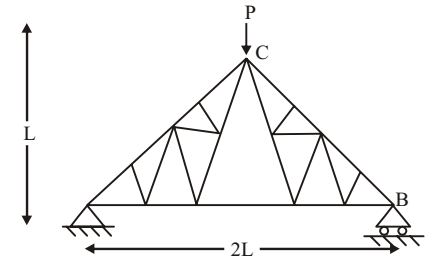

  1. Deflection of the point C is








  1. View Hint View Answer Discuss in Forum

    Deflection at C,

    δc =
    ∑ PPL
    		(Unit load method)
    AE

    All internal member have zero force
    ∴ δc =
    ∑ PPL
    AE

    =
    PL
    		+
    PL
    		+
    PL
    √2AE√2AE2AE

    =
    (2√2 + 1)
    PL
    2AE

    Correct Option: A

    Deflection at C,

    δc =
    ∑ PPL
    		(Unit load method)
    AE

    All internal member have zero force
    ∴ δc =
    ∑ PPL
    AE

    =
    PL
    		+
    PL
    		+
    PL
    √2AE√2AE2AE

    =
    (2√2 + 1)
    PL
    2AE